
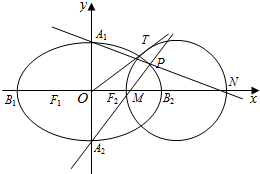
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{3}}}{2}$,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为$\frac{2\sqrt{5}}{5}$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{3}}}{2}$,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为$\frac{2\sqrt{5}}{5}$.分析 (1)设a=2m,c=$\sqrt{3}$m,则b=m.直线A2B2方程为mx-2my-2m2=0.由点到直线距离公式能求出m=1.由此能求出椭圆方程.
(2)由A1(0,1)A2(0,-1),设P(x0,y0),分别求出直线PA1和直线PA2,法一:设圆G的圆心为($\frac{1}{2}$($\frac{x0}{y0+1}$-$\frac{x0}{y0-1}$),0),利用圆的性质能证明线段OT的长度为定值2;法二:由切割线定理得OT2=OM•ON=4.从而得到线段OT的长度为定值2.
解答 解:(1)因为椭圆C的离心率e=$\frac{\sqrt{3}}{2}$,故设a=2m,c=$\sqrt{3}$m,则b=m.
直线A2B2方程为 bx-ay-ab=0,即mx-2my-2m2=0.
所以$\frac{2{m}^{2}}{\sqrt{{m}^{2}+4{m}^{2}}}$=$\frac{2\sqrt{5}}{5}$,解得m=1.
所以a=2,b=1,椭圆方程为$\frac{{x}^{2}}{4}$+y2=1.…(5分)
证明:(2)由(1)可知A1(0,1)A2(0,-1),设P(x0,y0),
直线PA1:y-1=$\frac{{y}_{0}-1}{{x}_{0}}$x,令y=0,得xN=-$\frac{{x}_{0}}{{y}_{0}-1}$,…(6分)
直线PA2:y+1=$\frac{{y}_{0}+1}{{x}_{0}}$x,令y=0,得xM=$\frac{{x}_{0}}{{y}_{0}+1}$,…(7分)
解法一:设圆G的圆心为($\frac{1}{2}$($\frac{{x}_{0}}{{y}_{0}+1}$-$\frac{{x}_{0}}{{y}_{0}-1}$),0),…(9分)
则r2=[$\frac{1}{2}$($\frac{{x}_{0}}{{y}_{0}+1}$-$\frac{{x}_{0}}{{y}_{0}-1}$)-$\frac{{x}_{0}}{{y}_{0}-1}$]2=$\frac{1}{4}$($\frac{{x}_{0}}{{y}_{0}+1}$+$\frac{{x}_{0}}{{y}_{0}-1}$)2.…(11分)
OG2=$\frac{1}{4}$($\frac{{x}_{0}}{{y}_{0}+1}$-$\frac{{x}_{0}}{{y}_{0}-1}$)2.
OT2=OG2-r2=$\frac{1}{4}$($\frac{{x}_{0}}{{y}_{0}+1}$-$\frac{{x}_{0}}{{y}_{0}-1}$)2-$\frac{1}{4}$($\frac{{x}_{0}}{{y}_{0}+1}$+$\frac{{x}_{0}}{{y}_{0}-1}$)2=$\frac{{{x}_{0}}^{2}}{1-{{y}_{0}}^{2}}$.…(13分)
而$\frac{{{x}_{0}}^{2}}{4}$+y02=1,所以x02=4(1-y02),所以OT2=4,…(15分)
所以OT=2,即线段OT的长度为定值2.…(16分)
解法二:OM•ON=|(-$\frac{{x}_{0}}{{y}_{0}-1}$)•$\frac{{x}_{0}}{{y}_{0}+1}$|=$\frac{{{x}_{0}}^{2}}{1-{{y}_{0}}^{2}}$,
而$\frac{{{x}_{0}}^{2}}{4}$+y02=1,所以x02=4(1-y02),所以OM•ON=4.
由切割线定理得OT2=OM•ON=4.
所以OT=2,即线段OT的长度为定值2.…(16分)
点评 本题考查椭圆方程的求法,是中档题,解题时要认真审题,注意椭圆、圆、点到直线距离公式、切割线定理等知识点的合理运用.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (2,$\frac{5}{2}$) | C. | (0,$\frac{5}{2}$) | D. | (-∞,$\frac{5}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{9\sqrt{3}}}{2}$ | D. | $\frac{{2\sqrt{3}}}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com