
分析 $\frac{1}{3}<x<\frac{1}{2}$是不等式m-1<x<m+1成立的一个充分非必要条件,可得$\left\{\begin{array}{l}{m-1≤\frac{1}{3}}\\{\frac{1}{2}≤m+1}\end{array}\right.$,等号不能同时成立,解出即可得出.
解答 解:∵$\frac{1}{3}<x<\frac{1}{2}$是不等式m-1<x<m+1成立的一个充分非必要条件,
∴$\left\{\begin{array}{l}{m-1≤\frac{1}{3}}\\{\frac{1}{2}≤m+1}\end{array}\right.$,且等号不能同时成立,
解得$-\frac{1}{2}≤m≤\frac{4}{3}$.
故答案为:$[-\frac{1}{2},\frac{4}{3}]$.
点评 本题考查了简易逻辑的判定方法、不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
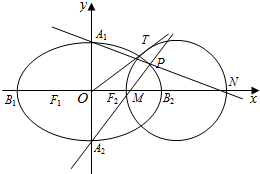 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{3}}}{2}$,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为$\frac{2\sqrt{5}}{5}$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{3}}}{2}$,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | $-\frac{1}{4}$ | C. | 4 | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
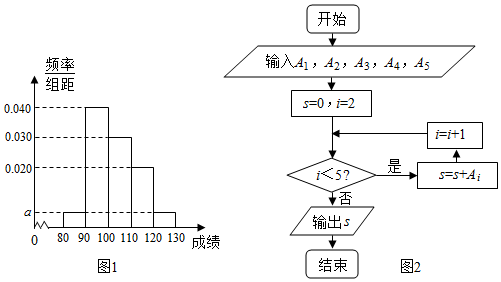
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,4) | B. | (2,3) | C. | (1,2) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | S=2,即5个数据的方差为2 | B. | S=2,即5个数据的标准差为2 | ||
| C. | S=10,即5个数据的方差为10 | D. | S=10,即5个数据的标准差为10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com