
如图所示,四棱锥P-ABCD中,底面ABCD是∠DAB=60°的菱形,侧面PAD为正三角形,其所在
平面垂直于底面ABCD.
(1)求证:AD⊥PB.
(2)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD?并证明你的结论.
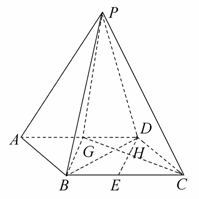
解析:(1)方法一,如图,取AD中点G,连接PG,BG,BD.
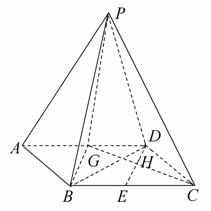
∵△PAD为等边三角形,∴PG⊥AD,
又∵平面PAD⊥平面ABCD,∴PG⊥平面ABCD.
在△ABD中,∠A=60°,AD=AB,∴△ABD为等边三角形,∴BG⊥AD,
∴AD⊥平面PBG,∴AD⊥PB.
方法二,如图,取AD中点G
∵△PAD为正三角形,∴PG⊥AD
又易知△ABD为正三角形
∴AD⊥BG.
又BG,PG为平面PBG内的两条相交直线,
∴AD⊥平面PBG.
∴AD⊥PB.
(2)连接CG与DE相交于H点,
在△PGC中作HF∥PG,交PC于F点,
∴FH⊥平面ABCD,
∴平面DHF⊥平面ABCD,
∵H是CG的中点,∴F是PC的中点,
∴在PC上存在一点F,即为PC的中点,使得平面DEF⊥平面ABCD.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
已知矩形ABCD的面积为8,当矩形ABCD周长最小时,沿对角线AC把△ACD折起,则三棱锥D-ABC的外接球表面积等于 ( )
A.8π B.16π
C.48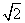 π D.不确定的实数
π D.不确定的实数
查看答案和解析>>
科目:高中数学 来源: 题型:
四面体ABCD中,有以下命题:
①若AC⊥BD,AB⊥CD,则AD⊥BC;
②若E、F、G分别是BC,AB,CD的中点,则∠EFG的大小等于异面直线AC与BD所成角的大小;
③若点O是四面体ABCD外接球的球心,则O在面ABD上的射影是△ABD的外心;
④若四个面是全等的三角形,则ABCD为正四面体.
其中正确命题序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com