考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:①令f(x)=2
-|x|,利用偶函数的定义f(-x)=f(x)即可判断出;
②令f(x)=1,T>0,利用周期函数的定义f(x+T)=f(x)即可判断出;
③容易验证x=2,4是函数的零点.利用函数零点判定存在定理可判断在区间(-1,0)时存在零点.
④画出函数函数g(x)=|log
2 x|-(
)
x在(0,+∞)的图象即可判断出.
解答:
解:①令f(x)=2
-|x|,则f(-x)=f(x),∴函数y=2
-|x|为偶函数;
②令f(x)=1,T>0,则f(x+T)=f(x)=1,∴函数y=1是周期函数;
③由函数f(x)=2
x-x
2,
∵f(2)=f(4)=0,∴x=2,4是函数的零点.
又f(0)=1>0,f(-1)=2
-1-(-1)
2=
-<0,∴f(0)f(-1)<0.
∴在区间(-1,0)时存在零点.
∴函数共有3个零点.因此不正确.
④画出函数函数g(x)=|log
2 x|-(
)
x在(0,+∞)的图象:
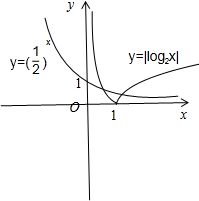
上恰有两个零点x
1,x
2.
不妨设x
1<x
2.
则0<x
1<1<x
2.
-log2x1=()x1,log
2x
2=
()x2.
∴log
2(x
1x
2)=
()x2-
()x1<0,
∴x
1•x
2<1.
因此正确.
综上可知:只有①②④正确.
故答案为:①②④.
点评:本题考查了函数奇偶性、函数零点判定定理、数形结合思想方法,属于中档题.




 记者在街上随机抽取10人调查其在一个月内接到的打扰性短信息次数,得统计的茎叶图如下:
记者在街上随机抽取10人调查其在一个月内接到的打扰性短信息次数,得统计的茎叶图如下: