
分析 (Ⅰ)设“前两个乒乓球所标数字之和为偶数”为事件A,“第三个乒乓球为奇数”为事件B,由此利用条件概率计算公式能求出前两个乒乓球所标数字之和为偶数的条件下,第三个乒乓球为奇数的概率.
(Ⅱ)ξ的可能取值为1,2,3,4.分别求出相应的概率,由此能求出随机变量ξ的分布列及数学期望.
解答 解:(Ⅰ)设“前两个乒乓球所标数字之和为偶数”为事件A,
“第三个乒乓球为奇数”为事件B,
则所求概率为$P(B\left|A\right.)=\frac{P(A•B)}{P(A)}=\frac{C_3^1A_2^2+A_2^2A_3^1}{C_4^1A_2^2A_3^1}=\frac{1}{2}$.
(Ⅱ)ξ的可能取值为1,2,3,4.
$P(ξ=1)=\frac{A_2^1}{A_5^1}=\frac{2}{5},P(ξ=2)=\frac{A_3^1A_2^1}{A_5^2}=\frac{3}{10},P(ξ=3)=\frac{A_3^2A_2^1}{A_5^3}=\frac{1}{5},P(ξ=4)=\frac{A_3^3A_2^1}{A_5^4}=\frac{1}{10}$,
ξ的分布列为
| ξ | 1 | 2 | 3 | 4 |
| P | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{1}{5}$ | $\frac{1}{10}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


科目:高中数学 来源: 题型:解答题
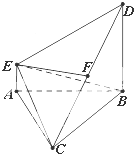 如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
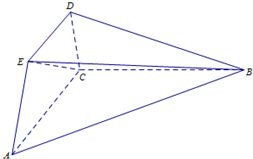 如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.
如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -2 | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{2}$ | -$\sqrt{2}$ | -1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+$\sqrt{2}$ | B. | 2-$\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | [1,2] | C. | [-2,0] | D. | [-2,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com