
| A. | 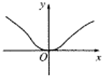 | B. |  | C. | 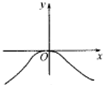 | D. | 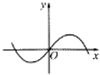 |
分析 分析函数奇偶性和x∈(0,$\frac{π}{2}$)时函数图象的位置,排除错误答案,可得结论.
解答 解:∵f(x)=($\frac{2}{1+{e}^{x}}$-1)cosx,
∴f(-x)=($\frac{2}{1+{e}^{-x}}$-1)cos(-x)=($\frac{{2e}^{x}}{1+{e}^{x}}$-1)cosx=-($\frac{2}{1+{e}^{x}}$-1)cosx=-f(x),
故函数f(x)为奇函数,故函数图象关于原点对称,可排除A,C,
又由当x∈(0,$\frac{π}{2}$),f(x)<0,函数图象位于第四象限,可排除D,
故选:B
点评 本题考查的知识点是函数的图象,由于函数非基本初等函数,故利用排除法,是解答的最佳选择.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,4] | B. | [2,4] | C. | [1,3] | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4500 | B. | 4505 | C. | 4514 | D. | 4519 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com