
| A. | b=7,c=3,C=30° | B. | a=20,b=30,C=30° | C. | b=4,c=2$\sqrt{3}$,C=60° | D. | b=5,c=4,C=45° |
分析 对于A,由正弦定理可得:sinB>1,可得三角形无解;
对于B,由余弦定理可得c为定值,三角形有一解;
对于C,由正弦定理可得:sinB=1,可求B=90°,A=30°,三角形有一解;
对于D,由正弦定理可得:sinB=$\frac{5\sqrt{2}}{8}$,结合B的范围,可求B有2解,本选项符合题意;
解答 解:对于A,∵b=7,c=3,C=30°,
∴由正弦定理可得:sinB=$\frac{bsinC}{c}$=$\frac{7×\frac{1}{2}}{3}$=$\frac{7}{6}$>1,无解;
对于B,∵a=20,b=30,C=30°,
∴由余弦定理可得c=$\sqrt{{a}^{2}+{b}^{2}-2abcosC}$=$\sqrt{400+900-2×20×30×\frac{\sqrt{3}}{2}}$=$\sqrt{1300-600\sqrt{3}}$,有一解;
对于C,∵b=4,c=2$\sqrt{3}$,C=60°,
∴由正弦定理可得:sinB=$\frac{bsinC}{c}$=$\frac{4×\frac{\sqrt{3}}{2}}{2\sqrt{3}}$=1,B=90°,A=30°,有一解;
对于D,∵b=5,c=4,C=45°,
∴由正弦定理可得:sinB=$\frac{bsinC}{c}$=$\frac{5×\frac{\sqrt{2}}{2}}{4}$=$\frac{5\sqrt{2}}{8}$,
又B为三角形的内角,
∴B∈(45°,180°),可得B有2解,本选项符合题意;
故选:D.
点评 此题属于解三角形的题型,涉及的知识有:正弦定理,三角形的边角关系,正弦函数的图象与性质,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥α,则m∥n | B. | 若m?α,n?α,m∥β,l∥β,则α∥β | ||
| C. | 若α⊥β,m?α,则m⊥β | D. | 若α⊥β,m⊥β,m?α,则m∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-1,\frac{1}{2}})$ | B. | $({-1,\frac{1}{2}})$ | C. | $({0,\frac{1}{2}})$ | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (1,3] | C. | (1,3) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
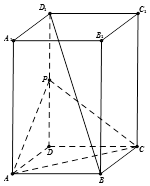 .如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
.如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±2\sqrt{2}$ | B. | 6 | C. | 2或6 | D. | -2或-6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30种 | B. | 36种 | C. | 42种 | D. | 48种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com