练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法中，正确的命题是（ ）

    A.以模型去拟合一组数据时，为了求出回归方程，设，将其变换后得到线性方程，则，的值分别是和0.3；

    B.事件为必然事件，则事件、是互为对立事件；

    C.设随机变量，若，则；

    D.甲、乙、丙、丁4个人到4个景点旅游，每人只去一个景点，设事件“4个人去的景点各不相同”，事件“甲独自去一个景点”，则.

    【答案】ACD

    【解析】

    根据回归方程，对立事件，正态分布的性质和条件概率公式，依次计算判断每个选项得到答案.

    ，两边取对数得到，故，的值分别是和0.3，A正确；

    B错误，举反例：随机投一个骰子，事件表示骰子点数为1,2,3,4，事件表示骰子点数为4,5,6，不是对立事件；

    根据对称性：，故，C正确；

    ，D正确.

    故选：ACD.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数（，是自然对数的底数）

    (Ⅰ) 设（其中是的导数），求的极小值；

    (Ⅱ) 若对，都有成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：

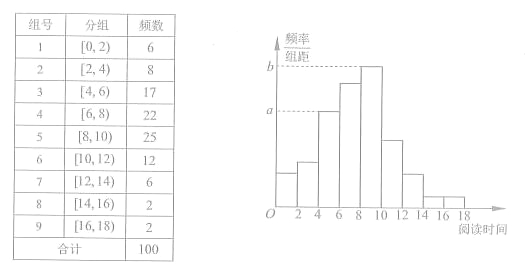
    （1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；

    （2）求频率分布直方图中的a，b的值；

    （3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组（只需写出结论）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知多面体中，，平面，，，，.

    （Ⅰ）证明：平面；

    （Ⅱ）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）求曲线在点处的切线方程；

    （Ⅱ）若函数在区间上单调递增，求实数的取值范围；

    （Ⅲ）设函数，其中.证明：的图象在图象的下方.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】矩形中，，，点为中点，沿将折起至，如图所示，点在面的射影落在上.

    （1）求证：面面；

    （2）求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年在印度尼西亚日惹举办的亚洲乒乓球锦标赛男子团体决赛中，中国队与韩国队相遇，中国队男子选手A，B，C，D，E依次出场比赛，在以往对战韩国选手的比赛中他们五人获胜的概率分别是0.8，0.8，0.8，0.75，0.7，并且比赛胜负相互独立.赛会釆用5局3胜制，先赢3局者获得胜利.

    （1）在决赛中，中国队以3∶1获胜的概率是多少？

    （2）求比赛局数的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在菱形中，，，对角线与交于点，点，分别在，上，满足，交于点.将沿折到的位置， .

    （Ⅰ）证明：；

    （Ⅱ）求与平面所成的角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义一个“希望结合”（）简称如下：为一个非空集合，它满足条件“若，则”。试问：在集合中，一共有多少个“希望子集合”？请说明理由。

    查看答案和解析>>

    同步练习册答案