
【题目】矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,沿
中点,沿![]() 将
将![]() 折起至
折起至![]() ,如图所示,点
,如图所示,点![]() 在面
在面![]() 的射影
的射影![]() 落在
落在![]() 上.
上.
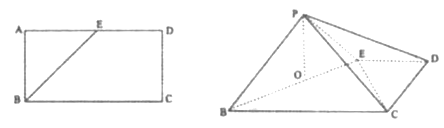
(1)求证:面![]() 面
面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)详见解析(2)![]()
【解析】
(1)首先可通过题目所给条件证出![]() 面
面![]() 即
即![]() ,再通过
,再通过![]() 和
和![]() 可证
可证![]() 面
面![]() ,最后即可证明出面
,最后即可证明出面![]() 面
面![]() ;
;
(2)首先可构造平面直角坐标系,然后求出面![]() 的法向量
的法向量![]() 和面
和面![]() 的法向量
的法向量![]() ,最后通过平面
,最后通过平面![]() 与平面
与平面![]() 所成锐二面角
所成锐二面角![]() 与
与![]() 互补即可得出结果。
互补即可得出结果。
(1)在四棱锥![]() 中,
中,![]() ,
,![]() ,从而有
,从而有![]() ,
,
又因为![]() 面
面![]() ,而
,而![]() 面
面![]() ,所以
,所以![]() ,
,
而![]() 、
、![]() 面
面![]() ,且
,且![]() ,由线面垂直定理可证
,由线面垂直定理可证![]() 面
面![]()
又![]() 面
面![]() ,由面面垂直判断定定理即证面
,由面面垂直判断定定理即证面![]() 面
面![]()
(2)由条件知![]() 面
面![]() ,过点
,过点![]() 做
做![]() 的平行线
的平行线![]() ,又由(1)知
,又由(1)知![]() 面
面![]() ,
,
以![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
如图所示:
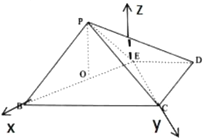
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
面![]() 的一个法向量为
的一个法向量为![]() ,
,
设面![]() 的法向量为
的法向量为![]() ,则有
,则有 ,
,
从而可得面![]() 的一个法向量为
的一个法向量为![]() ,
,![]() ,
,
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,与
,与![]() 互补,则
互补,则![]() ,
,
故平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() 。
。


科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,现将
,现将![]() 沿
沿![]() 折到
折到![]() 的位置,连结
的位置,连结![]() ,
,![]() ,如图2.
,如图2.
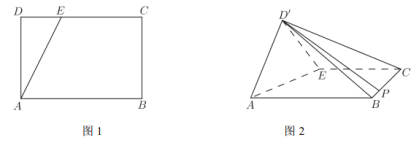
(1)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,证明:
,证明:![]() ;
;
(2)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() .若二面角
.若二面角![]() 为
为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() 丄底面
丄底面![]() .
.
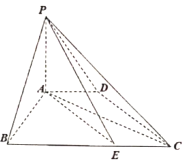
(1)证明:平面![]() 平面
平面![]() ;
;
(2)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四棱锥
把四棱锥![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的命题是( )
A.以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和0.3;
和0.3;
B.事件![]() 为必然事件,则事件
为必然事件,则事件![]() 、
、![]() 是互为对立事件;
是互为对立事件;
C.设随机变量![]() ,若
,若![]() ,则
,则![]() ;
;
D.甲、乙、丙、丁4个人到4个景点旅游,每人只去一个景点,设事件![]() “4个人去的景点各不相同”,事件
“4个人去的景点各不相同”,事件![]() “甲独自去一个景点”,则
“甲独自去一个景点”,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知动直线
中,已知动直线![]() 的参数方程:
的参数方程:![]() ,(
,(![]() 为参数,
为参数,![]() ) ,以坐标原点为极点,
) ,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 恰好有2个公共点时,求直线
恰好有2个公共点时,求直线![]() 的一般方程.
的一般方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com