
 已知空间几何体CBEADF如图所示,底面AEFD为矩形,平面BEFC⊥平面AEFD,∠CFE=∠BEF=90°,其中AE+BE=AD=2,DF+CF=4.
已知空间几何体CBEADF如图所示,底面AEFD为矩形,平面BEFC⊥平面AEFD,∠CFE=∠BEF=90°,其中AE+BE=AD=2,DF+CF=4.分析 (1)计算CF=3,得出FG=1,利用平行四边形的判定与性质得出DG∥AB,故而DG∥平面ABC;
(2)利用体积求出BE,建立坐标系,计算$\overrightarrow{BF}$和$\overrightarrow{CA}$的夹角得出异面直线所成角的大小.
解答 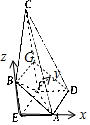 (1)证明:当AE=1时,BE=1,DF=AE=1,∴CF=3,
(1)证明:当AE=1时,BE=1,DF=AE=1,∴CF=3,
∴FG=$\frac{1}{3}$CF=1,
∴BE$\stackrel{∥}{=}$FG,
∴四边形BEFG是平行四边形,
∴BG$\stackrel{∥}{=}$EF,又AD$\stackrel{∥}{=}$EF,
∴BG$\stackrel{∥}{=}$AD,
∴四边形ABGD是平行四边形,
∴DG∥AB,又AB?平面ABC,DG?平面ABC,
∴DG∥平面ABC.
(2)解:∵平面BEFC⊥平面AEFD,∠BEF=90°,平面BEFC∩平面AEFD=EF,
∴BE⊥平面AEFD,
设AE=a,则BE=2-a,
∴VE-ABF=VB-AEF=$\frac{1}{3}×\frac{1}{2}×2×a×(2-a)$=$\frac{1}{3}$,
解得a=1,∴BE=AE=1,CF=3,
以E为原点,以EA,EF,EB为坐标轴建立空间坐标系,
则A(1,0,0),B(0,0,1),F(0,2,0),C(0,2,3),
∴$\overrightarrow{BF}$=(0,2,-1),$\overrightarrow{CA}$=(1,-2,-3),
∴cos<$\overrightarrow{BF},\overrightarrow{CA}$>=$\frac{\overrightarrow{BF}•\overrightarrow{CA}}{|\overrightarrow{BF}||\overrightarrow{CA}|}$=$\frac{-4+3}{\sqrt{5}•\sqrt{14}}$=-$\frac{\sqrt{70}}{70}$,
∴直线BF与CA所成角的余弦值为|cos<$\overrightarrow{BF},\overrightarrow{CA}$>|=$\frac{\sqrt{70}}{70}$.
点评 本题考查了线面平行的判定,异面直线所成角的计算,属于中档题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:选择题
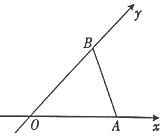 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中OA=OB=1,则原平面图形的面积为( )
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中OA=OB=1,则原平面图形的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
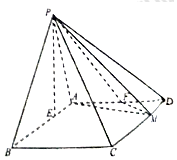 在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.
在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com