
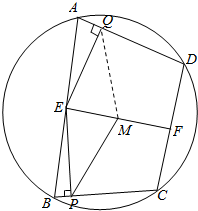
 已知E、F是圆内接四边形ABCD对边AB、CD的中点,M是EF的中点,自E分别作BC、AD的垂线,垂足记为P、Q.求证:MP=MQ.
已知E、F是圆内接四边形ABCD对边AB、CD的中点,M是EF的中点,自E分别作BC、AD的垂线,垂足记为P、Q.求证:MP=MQ. 分析 过F、T作BC、AD的垂线,垂直足为X、Y、P、Q,则TX和TY为MP和NQ的垂直平分线,推导出M、N、Q、P四点共圆,得到T是圆MNQP的圆心,由此能证明TM=TN.
解答 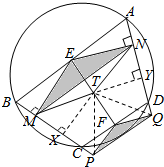 证明:如图,过F、T作BC、AD的垂线,垂直足为X、Y、P、Q,
证明:如图,过F、T作BC、AD的垂线,垂直足为X、Y、P、Q,
如图连结辅助线,则TX和TY为MP和NQ的垂直平分线,
由四点共圆知:
EN=$\frac{1}{2}AB•sinA$,EM=$\frac{1}{2}AB•sinB$,FQ=$\frac{1}{2}CD•sinB$,FQ=$\frac{1}{2}CD•sinB$,FP=$\frac{1}{2}CD•sinA$,
∴$\frac{EN}{EM}=\frac{FP}{FQ}$,又由EN∥FQ,EM∥FP,∴∠NEM=∠PFQ,
∴△NEM∽△PFQ,∴∠ENM=∠FPQ,
∴∠MNQ+∠QPM=∠MNQ+∠ENM+∠FPM=90°+90°=180°,
∴M、N、Q、P四点共圆,
∴T是圆MNQP的圆心,
∴TM=TN.
点评 本题考查线段相等的证明,是中档题,解题时要认真审题,注意四点共圆的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,4] | B. | (-∞,4] | C. | [-4,0)∪(0,4] | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com