
分析 直线$\left\{\begin{array}{l}{x=1+t}\\{y=-4+t}\end{array}\right.$(t为参数),消去参数可得普通方程.由圆锥曲线$\left\{\begin{array}{l}{x=\frac{a}{cosθ}}\\{y=3tanθ}\end{array}\right.$(θ为参数,a>0),可得$(\frac{x}{a})^{2}$-$(\frac{y}{3})^{2}$=1,可得右焦点$(\sqrt{{a}^{2}+9},0)$,代入直线方程解出即可得出.
解答 解:直线$\left\{\begin{array}{l}{x=1+t}\\{y=-4+t}\end{array}\right.$(t为参数),消去参数可得普通方程:x-y-5=0.
由圆锥曲线$\left\{\begin{array}{l}{x=\frac{a}{cosθ}}\\{y=3tanθ}\end{array}\right.$(θ为参数,a>0),可得$(\frac{x}{a})^{2}$-$(\frac{y}{3})^{2}$=$\frac{1}{co{s}^{2}θ}$-tan2θ=$\frac{1-si{n}^{2}θ}{co{s}^{2}θ}$=1,即$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{9}$=1.
可得右焦点$(\sqrt{{a}^{2}+9},0)$,代入直线方程可得:$\sqrt{{a}^{2}+9}$-0-5=0,化为a2=16,a>0,解得a=4.
故答案为:4.
点评 本题考查了参数方程化为普通方程、双曲线的标准方程及其性质、三角函数化简求值,考查了推理能力与计算能力,属于中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
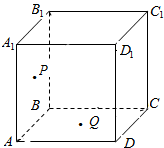 如图所示,已知P,Q是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.
如图所示,已知P,Q是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 与x轴、y轴都相交 | B. | 与x轴相交,与y轴不相交 | ||
| C. | 与x轴不相交,与y轴相交 | D. | 与x轴、y轴都不相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}$+y2=1 | B. | $\frac{y^2}{4}$+x2=1 | C. | $\frac{y^2}{8}$+$\frac{x^2}{5}$=1 | D. | $\frac{x^2}{8}$+$\frac{y^2}{5}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 芯片甲 | 8 | 12 | 40 | 32 | 8 |
| 芯片乙 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com