
分析 根据平面向量的坐标表示与运算法则,利用数量积的定义,即可求出对应向量的坐标表示与模长、夹角的余弦值.
解答 解:(1)$\overrightarrow{AB}$=(5,-12)-(-3,-4)=(8,-8),
∴$\left|\overrightarrow{AB}\right|=\sqrt{{8}^{2}+{(-8)}^{2}}=8\sqrt{2}$;
(2)$\overrightarrow{OC}=(-3,-4)+(5,-12)=(2,-16)$,
$\overrightarrow{OD}=(-3,-4)-(5,-12)=(-8,8)$;
(3)$\overrightarrow{OA}?\overrightarrow{OB}=(-3,-4)?(5,-12)=-3×5+(-4)×(-12)=33$,
设$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ,
则$cosθ=\frac{\overrightarrow{OA}?\overrightarrow{OB}}{\left|\overrightarrow{OA}\right|\left|\overrightarrow{OB}\right|}=\frac{33}{5×12}=\frac{33}{65}$.
点评 本题考查了平面向量的坐标表示与利用数量积求模长、夹角余弦值的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
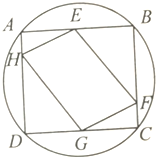 如图所示,正方形ABCD内接于圆O,且AE=BE=CG=DG,AH=CF=$\frac{1}{4}$AD,则往圆O内投掷一点,该点落在四边形EFGH内的概率为$\frac{1}{π}$.
如图所示,正方形ABCD内接于圆O,且AE=BE=CG=DG,AH=CF=$\frac{1}{4}$AD,则往圆O内投掷一点,该点落在四边形EFGH内的概率为$\frac{1}{π}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 曲线的切线 | B. | 曲线的切线的斜率 | ||
| C. | 曲线y=f(x)的切线的斜率 | D. | 曲线y=f(x)在点(x0,f(x0))处切线的斜率 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com