
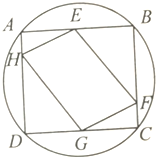
 如图所示,正方形ABCD内接于圆O,且AE=BE=CG=DG,AH=CF=$\frac{1}{4}$AD,则往圆O内投掷一点,该点落在四边形EFGH内的概率为$\frac{1}{π}$.
如图所示,正方形ABCD内接于圆O,且AE=BE=CG=DG,AH=CF=$\frac{1}{4}$AD,则往圆O内投掷一点,该点落在四边形EFGH内的概率为$\frac{1}{π}$. 科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}$+y2=1 | B. | $\frac{y^2}{4}$+x2=1 | C. | $\frac{y^2}{8}$+$\frac{x^2}{5}$=1 | D. | $\frac{x^2}{8}$+$\frac{y^2}{5}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 芯片甲 | 8 | 12 | 40 | 32 | 8 |
| 芯片乙 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${log_{\frac{1}{2}}}({2^{a_3}}+{2^{a_7}})$有最小值-3 | B. | ${log_{\frac{1}{2}}}({2^{a_3}}+{2^{a_7}})$有最小值3 | ||
| C. | ${log_{\frac{1}{2}}}({2^{a_3}}+{2^{a_7}})$有最大值-3 | D. | ${log_{\frac{1}{2}}}({2^{a_3}}+{2^{a_7}})$有最大值3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [0,+∞) | C. | [0,1] | D. | [0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com