
分析 (Ⅰ)利用绝对值三角不等式,结合基本不等式证明:f(x)≥2$\sqrt{2}$;
(Ⅱ)求出f(x)min=3,若?x∈R,$f(x)≥{t^2}-\frac{1}{2}t$恒成立,则只需$f{(x)_{min}}=3≥{t^2}-\frac{1}{2}t⇒2{t^2}-t-6≤0⇒-\frac{3}{2}≤t≤2$.
解答 (Ⅰ)证明:∵m>0,$f(x)=|{2x-\frac{2}{m}}|+|{2x+m}|≥|{\frac{2}{m}+m}|=\frac{2}{m}+m≥2\sqrt{2}$,
当$\frac{2}{m}=m$即$m=\sqrt{2}$时取“=”号…(5分)
(Ⅱ)解:当m=2时,f(x)=|2x-1|+|2x+2|≥|(2x-1)-(2x+2)|=3
则f(x)min=3,若?x∈R,$f(x)≥{t^2}-\frac{1}{2}t$恒成立,
则只需$f{(x)_{min}}=3≥{t^2}-\frac{1}{2}t⇒2{t^2}-t-6≤0⇒-\frac{3}{2}≤t≤2$,
综上所述实数t的取值范围是$-\frac{3}{2}≤t≤2$.…(10分)
点评 本题考查绝对值三角不等式,考查基本不等式的运用,考查恒成立问题,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4}$,$\frac{4}{5}$] | B. | ($\frac{1}{4}$,1] | C. | [-$\frac{1}{3}$,1] | D. | [0,$\frac{4}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
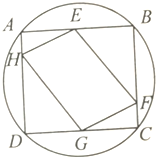 如图所示,正方形ABCD内接于圆O,且AE=BE=CG=DG,AH=CF=$\frac{1}{4}$AD,则往圆O内投掷一点,该点落在四边形EFGH内的概率为$\frac{1}{π}$.
如图所示,正方形ABCD内接于圆O,且AE=BE=CG=DG,AH=CF=$\frac{1}{4}$AD,则往圆O内投掷一点,该点落在四边形EFGH内的概率为$\frac{1}{π}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com