
分析 (Ⅰ)求出函数的导数,计算f′(π),f(π),求出切线方程即可;
(Ⅱ)令g(x)=f(x)-$\frac{1}{3}$x3,$x∈(0\;,\;\frac{π}{2})$,求出g(x)的单调性,从而证出结论;
(Ⅲ)问题转化为k<$\frac{sinx}{x}$对$x∈(0\;,\;\frac{π}{2})$恒成立,令m(x)=$\frac{sinx}{x}$,$x∈(0\;,\;\frac{π}{2})$,根据函数的单调性求出k的最大值即可.
解答 解:(Ⅰ)f(x)=sinx-xcosx,f′(x)=xsinx,
f′(π)=0,f(π)=π,
故切线方程是y-π=0;
(Ⅱ)证明:令g(x)=f(x)-$\frac{1}{3}$x3,$x∈(0\;,\;\frac{π}{2})$,
g′(x)=x(sinx-x),令h(x)=sinx-x,h′(x)=cosx-1<0,
∴h(x)在$x∈(0\;,\;\frac{π}{2})$递减,故h(x)<h(0)=0,
∴g′(x)<0,g(x)递减,
∴g(x)<g($\frac{π}{2}$)=$\frac{24{-π}^{3}}{24}$<0,
故当$x∈(0\;,\;\frac{π}{2})$时,$f(x)<\frac{1}{3}{x^3}$成立;
(Ⅲ)若f(x)>kx-xcosx对$x∈(0\;,\;\frac{π}{2})$恒成立,
即k<$\frac{sinx}{x}$对$x∈(0\;,\;\frac{π}{2})$恒成立,
令m(x)=$\frac{sinx}{x}$,$x∈(0\;,\;\frac{π}{2})$,
m′(x)=$\frac{xcosx-sinx}{{x}^{2}}$<0,
∴m(x)在(0,$\frac{π}{2}$)递减,
m(x)>m($\frac{π}{2}$)=$\frac{2}{π}$,
故k≤$\frac{2}{π}$.k的最大值是$\frac{2}{π}$.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及函数恒成立,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
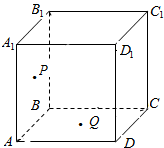 如图所示,已知P,Q是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.
如图所示,已知P,Q是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 直平行六面体ABCD-A1B1C1D1的棱长均为2,∠BAD=60°,则平面A1DC1与平面ABCD所成角的大小为arcsin$\frac{2\sqrt{5}}{5}$.
直平行六面体ABCD-A1B1C1D1的棱长均为2,∠BAD=60°,则平面A1DC1与平面ABCD所成角的大小为arcsin$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 芯片甲 | 8 | 12 | 40 | 32 | 8 |
| 芯片乙 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com