
ЎѕМвДїЎїОЄБЛЅвґєјѕЦзТ№ОВІоґуРЎУлЦЦЧУ·ўСї¶аЙЩЦ®јдµД№ШПµЈ¬ПЦґУ4ФВµД30МмЦРЛж»ъМфСЎБЛ5МмЅшРРСРѕїЈ¬ЗТ·Ц±рјЗВјБЛГїМмЦзТ№ОВІоУлГїМмГї50їЕЦЦЧУЅюЕЭєуµД·ўСїКэЈ¬µГµЅИзПВ±нёсЈє
ИХЖЪ | 4ФВ1ИХ | 4ФВ6ИХ | 4ФВ12ИХ | 4ФВ19ИХ | 4ФВ27ИХ |
ОВІо | 2 | 3 | 5 | 4 | 1 |
·ўСїКэ | 9 | 11 | 15 | 13 | 7 |
ЈЁ1Ј©ґУХв5МмЦРИОСЎ2МмЈ¬јЗ·ўСїµДЦЦЧУКэ·Ц±рОЄ![]() Ј¬ЗуКВјюЎ°
Ј¬ЗуКВјюЎ°![]() ѕщРЎУЪ13Ў±µДёЕВКЈ»
ѕщРЎУЪ13Ў±µДёЕВКЈ»
ЈЁ2Ј©Иф4ФВ30ИХЦзТ№ОВІоОЄ![]() Ј¬ЗлёщѕЭ
Ј¬ЗлёщѕЭ![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМ
µДПЯРФ»Ш№й·ЅіМ![]() №АјЖёГМмЦЦЧУЅюЕЭєуµД·ўСїКэ.
№АјЖёГМмЦЦЧУЅюЕЭєуµД·ўСїКэ.
ІОїј№«КЅЈє  Ј¬
Ј¬ ![]() .
.
Ўѕґр°ёЎїЈЁ1Ј©![]() ЈЁ2Ј©17їЕ.
ЈЁ2Ј©17їЕ.
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁ1Ј©ПИБРѕЩЛщУРµД»щ±ѕКВјю,№І10ёц,ФЩМфіцВъЧг Ў°![]() ѕщРЎУЪ13Ў± КВјю,№І3ёц,ЧоєуёщѕЭ№ЕµдёЕРНёЕВК№«КЅЗуёЕВКЈЁ2Ј©АыУГІОїј№«КЅЗуіц
ѕщРЎУЪ13Ў± КВјю,№І3ёц,ЧоєуёщѕЭ№ЕµдёЕРНёЕВК№«КЅЗуёЕВКЈЁ2Ј©АыУГІОїј№«КЅЗуіц![]() ТФј°
ТФј°![]() ,ФЩЗуіцЧФ±дБїОЄ6К±¶ФУ¦єЇКэЦµ
,ФЩЗуіцЧФ±дБїОЄ6К±¶ФУ¦єЇКэЦµ
КФМвЅвОцЈєЅвЈєЈЁ1Ј©ЛщУРµД»щ±ѕКВјюОЄ (9Ј¬11)Ј¬(9Ј¬15)Ј¬(9Ј¬13)Ј¬(9Ј¬7)Ј¬(11Ј¬15)Ј¬(11Ј¬13)Ј¬ (11Ј¬7)Ј¬(15Ј¬13)Ј¬(15Ј¬7)Ј¬(13Ј¬7)Ј¬№І10ёцЈ®
ЙиЎ°mЈ¬nѕщРЎУЪ13Ў±ОЄКВјюAЈ¬ФтКВјюA°ьє¬µД»щ±ѕКВјюОЄ (9Ј¬11)Ј¬(9Ј¬7)Ј¬(11Ј¬7)Ј¬№І3ёцЈ¬№ККВјюЎ°![]() ѕщРЎУЪ13Ў±µДёЕВК
ѕщРЎУЪ13Ў±µДёЕВК![]() .
.
ЈЁ2Ј©УЙКэѕЭµГ, ![]() ,
, ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
ЛщТФ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
ЛщТФ![]() Ј¬
Ј¬
ЛщТФ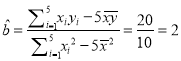 Ј¬
Ј¬
![]() Ј¬
Ј¬
ЛщТФ![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМОЄ
µДПЯРФ»Ш№й·ЅіМОЄ![]() .
.
µ±![]() К±Ј¬
К±Ј¬ ![]() Ј¬
Ј¬
ТтґЛЈ¬Иф4ФВ30ИХЦзТ№ОВІоОЄ![]() Ј¬ФтёГМмЦЦЧУЅюЕЭєуµД·ўСїКэґуФјОЄ17їЕ.
Ј¬ФтёГМмЦЦЧУЅюЕЭєуµД·ўСїКэґуФјОЄ17їЕ.


 AјУЅрМв ПµБРґр°ё
AјУЅрМв ПµБРґр°ё И«УЕІвКФѕнПµБРґр°ё
И«УЕІвКФѕнПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄПтБї ![]() =ЈЁ©Ѓ2Ј¬1Ј©Ј¬
=ЈЁ©Ѓ2Ј¬1Ј©Ј¬ ![]() =ЈЁxЈ¬yЈ©
=ЈЁxЈ¬yЈ©
ЈЁ1Ј©ИфxЈ¬y·Ц±р±нКѕЅ«Т»Г¶ЦКµШѕщФИµДХэ·ЅМеч»ЧУЈЁБщёцГжµДµгКэ·Ц±рОЄ1Ј¬2Ј¬3Ј¬4Ј¬5Ј¬6Ј©ПИєуЕЧЦАБЅґОК±µЪТ»ґОЎўµЪ¶юґОіцПЦµДµгКэЈ¬ЗуВъЧг ![]() =©Ѓ1µДёЕВКЈ»
=©Ѓ1µДёЕВКЈ»
ЈЁ2Ј©ИфxЈ¬yФЪБ¬РшЗшјд[1Ј¬6]ЙПИЎЦµЈ¬ЗуВъЧг ![]() Јј0µДёЕВКЈ®
Јј0µДёЕВКЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ ![]() µДЦµУтОЄЈЁ©ЃЎЮЈ¬0]ЎИ[4Ј¬+ЎЮЈ©Ј¬ФтaµДЦµКЗЈЁ Ј©
µДЦµУтОЄЈЁ©ЃЎЮЈ¬0]ЎИ[4Ј¬+ЎЮЈ©Ј¬ФтaµДЦµКЗЈЁ Ј©
A.![]()
B.![]()
C.1
D.2
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБРёчЧйєЇКэКЗН¬Т»єЇКэµДКЗЈЁ Ј©
A.![]() Ул
Ул ![]()
B.![]() УлgЈЁxЈ©=2x©Ѓ1
УлgЈЁxЈ©=2x©Ѓ1
C.fЈЁxЈ©=x0УлgЈЁxЈ©=1
D.fЈЁxЈ©=x2©Ѓ2x©Ѓ1УлgЈЁtЈ©=t2©Ѓ2t©Ѓ1
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБРєЇКэЦРЈ¬јИКЗЖжєЇКэУЦКЗФцєЇКэµДКЗЈЁ Ј©
A.y=x+1
B.y=©Ѓx2
C.y=x|x|
D.y=x©Ѓ1
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() .
.
ЈЁ1Ј©µ±![]() К±Ј¬ЗуЗъПЯ
К±Ј¬ЗуЗъПЯ![]() ФЪ
ФЪ![]() ґ¦µДЗРПЯ·ЅіМЈ»
ґ¦µДЗРПЯ·ЅіМЈ»
ЈЁ2Ј©МЦВЫ![]() µДµҐµчРФЈ»
µДµҐµчРФЈ»
ЈЁ3Ј©Йи№э![]() БЅµгµДЦ±ПЯµДР±ВКОЄ
БЅµгµДЦ±ПЯµДР±ВКОЄ![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]() Ўў
Ўў![]() ОЄЗъПЯ
ОЄЗъПЯ![]() ЙПµДИОТвБЅµгЈ¬ІўЗТ
ЙПµДИОТвБЅµгЈ¬ІўЗТ![]() Ј¬Иф
Ј¬Иф![]() єгіЙБўЈ¬Ц¤ГчЈє
єгіЙБўЈ¬Ц¤ГчЈє ![]() .
.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБРЛДёцЅбВЫЦРЈє
ЈЁ1Ј©Из№ыБЅёцєЇКэ¶јКЗФцєЇКэЈ¬ДЗГґХвБЅёцєЇКэµД»эФЛЛгЛщµГєЇКэОЄФцєЇКэЈ»
ЈЁ2Ј©ЖжєЇКэfЈЁxЈ©ФЪ[0Ј¬+ЎЮЈ©ЙПКЗФцєЇКэЈ¬ФтfЈЁxЈ©ФЪRЙПОЄФцєЇКэЈ»
ЈЁ3Ј©јИКЗЖжєЇКэУЦКЗЕјєЇКэµДєЇКэЦ»УРТ»ёцЈ»
ЈЁ4Ј©ИфєЇКэfЈЁxЈ©µДЧоРЎЦµКЗaЈ¬ЧоґуЦµКЗbЈ¬ФтfЈЁxЈ©ЦµУтОЄ[aЈ¬b]Ј®
ЖдЦРХэИ·ЅбВЫµДРтєЕОЄ Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЦ±ПЯlЈєy=3x+3Ј®
ЈЁ1Ј©ЗуµгPЈЁ5Ј¬3Ј©№ШУЪЦ±ПЯlµД¶ФіЖµгPЎдµДЧш±кЈ»
ЈЁ2Ј©ЗуЦ±ПЯl1Јєx©Ѓy©Ѓ2=0№ШУЪЦ±ПЯlµД¶ФіЖЦ±ПЯl2µД·ЅіМЈ»
ЈЁ3Ј©ТСЦЄµгMЈЁ2Ј¬6Ј©Ј¬КФФЪЦ±ПЯlЙПЗуТ»µгNК№µГ|NP|+|NM|µДЦµЧоРЎЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЧФ±дБїxЈ¬yВъЧг Фтµ±3ЎЬSЎЬ5К±Ј¬zЈЅ3xЈ«2yµДЧоґуЦµµД±д»Ї·¶О§ОЄ________Ј®
Фтµ±3ЎЬSЎЬ5К±Ј¬zЈЅ3xЈ«2yµДЧоґуЦµµД±д»Ї·¶О§ОЄ________Ј®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com