③④
分析:判断命题①,可以举一个例子,如函数f(x)=x
3,在x=0处的导数为0,但函数在x=0处无极值;
命题②中的直线过定点(0,1),保证b
2≥1,即b≥1或b≤-1的值,都能使点(0,1)在曲线上或其内部;
命题③采用反证法,假设a、b、c都小于2,三个式子相加后重新组合,运用基本不等式可得到与假设矛盾;
命题④转化成“不存在x∈R,使得|x-a|+|x+1|≤2”成立,然后求a的范围问题直接求解复杂,考虑绝对值的几何意义解决.
解答:命题①,设函数f(x)=x
3,f
′(0)=0,函数f(x)在x=0处无极值,所以命题①不正确.
命题②,不论m为何值,直线y=mx+1恒过定点(0,1),所以只要b
2≥1,点(0,1)一定在椭圆
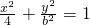
内部,所以
直线y=mx+1均与曲线
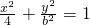
有公共点,此时b≥1或b≤-1,所以命题②不正确.
命题③,假设a、b、c均小于2,即
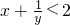
,
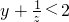
,
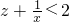
,则

,
而
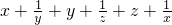
=

≥

(当且仅当x=y=z=1时等号成立),与假设矛盾,所以,若

,则a、b、c中至少有一个不小于2成立,故命题③正确.
命题④,若命题“存在x∈R,使得|x-a|+|x+1|≤2”是假命题,即“不存在x∈R,使得|x-a|+|x+1|≤2”成立,结合绝对值的几何意义,|x-a|+|x+1|看作数轴上实数x对应的动点X到两实数a和-1所对应定点的距离,若实数a对应的点到实数-1对应点的距离大于2,即|a+1|>2,则数轴上不存在实数x对应的动点到a和-1所对应定点的距离和小于等于2,即“不存在x∈R,使得|x-a|+|x+1|≤2”成立,故命题④正确.
故答案为③④.
点评:本题考查命题的真假判断与应用,解答的关键是每个命题的命题意图,命题①说明了导函数为0的点不一定是极值点;命题②考查了数形结合的思想方法;命题③考查了含有“至少”、“至多”、“存在”等一系列问题的常用证法(反证法);命题④体现了转化法这种数学思想方法.该题涉及知识点多,处理方法灵活.

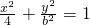 有公共点,则b≥1;
有公共点,则b≥1; ,则a、b、c中至少有一个不小于2;
,则a、b、c中至少有一个不小于2;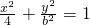 内部,所以
内部,所以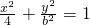 有公共点,此时b≥1或b≤-1,所以命题②不正确.
有公共点,此时b≥1或b≤-1,所以命题②不正确.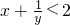 ,
,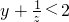 ,
,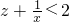 ,则
,则 ,
,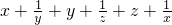 =
= ≥
≥ (当且仅当x=y=z=1时等号成立),与假设矛盾,所以,若
(当且仅当x=y=z=1时等号成立),与假设矛盾,所以,若 ,则a、b、c中至少有一个不小于2成立,故命题③正确.
,则a、b、c中至少有一个不小于2成立,故命题③正确.
