
分析 (Ⅰ)由椭圆$\frac{{x}^{2}}{2}$+y2=1焦点在x轴上,右焦点F2(1,0),设直线l的方程为:y=x-1,代入椭圆方程,利用两点之间的距离公式,求得丨AB丨,根据三角形的面积公式求得点P到直线l的距离为d,利用点到直线的距离公式与d比较即可求得P点坐标;
(Ⅱ)△ABF1的内切圆的半径为r,${S}_{AB{F}_{1}}$=$\frac{1}{2}$4a×r,要使内切圆的面积最大,即使得△ABF1最大,将直线方程代入椭圆方程,利用韦达定理,点到直线的距离公式及基本不等式的性质,即可求得得△ABF1最大值,求得内切圆的半径及面积和直线l的方程.
解答 解:(Ⅰ)由题意可知:椭圆$\frac{{x}^{2}}{2}$+y2=1焦点在x轴上,右焦点F2(1,0),
设直线l的方程为:y=x-1,则$\left\{\begin{array}{l}{y=x-1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:3x2-4x=0,
解得:x1=0,x2=$\frac{4}{3}$,
则丨AB丨=$\sqrt{1+{k}^{2}}$•丨x1-x2丨=$\frac{4}{3}$$\sqrt{2}$,
设点P到直线l的距离为d,则S△ABP=$\frac{1}{2}$•丨AB丨•d=$\frac{1}{2}$×$\frac{4}{3}$$\sqrt{2}$×d=$\frac{{2\sqrt{5}-2}}{3}$,
解得:d=$\frac{\sqrt{5}-1}{\sqrt{2}}$,
设P(x0,y0),则P到直线l的距离d=$\frac{丨{x}_{0}-{y}_{0}-1丨}{\sqrt{2}}$,
令t=x0-y0-1,由$\frac{{x}_{0}^{2}}{2}+{y}_{0}^{2}=1$,代入整理得:x02+2(x0-1-t)2=2,
化简整理得:3x02-4(1+t)x0+2t2+4t=0,
由△≥0,解得:-$\sqrt{3}$-1≤t≤-$\sqrt{3}$+1,
当-$\sqrt{3}$-1≤t<0,椭圆上方的点到直线l的距离的最大值为$\frac{\sqrt{3}+1}{\sqrt{2}}$>$\frac{\sqrt{5}-1}{\sqrt{2}}$,
则椭圆上存在两个这样的点P,使得△ABP的面积S△ABP=$\frac{{2\sqrt{5}-2}}{3}$,
当0≤t≤-$\sqrt{3}$+1,椭圆下方的点到直线l的距离的最大值为$\frac{\sqrt{3}+1}{\sqrt{2}}$<$\frac{\sqrt{5}-1}{\sqrt{2}}$,
则椭圆下方不存在这样的P点,使得△ABP的面积S△ABP=$\frac{{2\sqrt{5}-2}}{3}$,
综上可知:椭圆上存在这样的P点有二个;
(Ⅱ)△ABF1的内切圆的半径为r,${S}_{AB{F}_{1}}$=$\frac{1}{2}$(丨AF1丨+丨BF1丨+丨AB丨)×r=$\frac{1}{2}$4a×r,
∴要使内切圆的面积最大,即使得△ABF1最大,…9分
设直线l:x=my+1,
∴$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:(m2+2)y2+2my-1=0…10分
由△=8(1+m2)>0,
丨y1-y2丨=$\frac{\sqrt{△}}{{m}^{2}+2}$=$\frac{2\sqrt{2}\sqrt{1+{m}^{2}}}{{m}^{2}+2}$,…11分
设点F1到直线l的距离为h则:${S}_{AB{F}_{1}}$=$\frac{1}{2}$丨AB丨×h=$\frac{1}{2}$$\sqrt{1+{m}^{2}}$$\frac{2\sqrt{2}\sqrt{1+{m}^{2}}}{{m}^{2}+2}$$\frac{丨-(-1)+m×0+1丨}{\sqrt{1+{m}^{2}}}$=$\frac{2\sqrt{2}\sqrt{1+{m}^{2}}}{{m}^{2}+2}$,…13分
令t=$\sqrt{1+{m}^{2}}$,t≥0,则${S}_{AB{F}_{1}}$=$\frac{2\sqrt{2}t}{{t}^{2}+1}$=$\frac{2\sqrt{2}}{t+\frac{1}{t}}$≤$\frac{2\sqrt{2}}{2\sqrt{t•\frac{1}{t}}}$=$\sqrt{2}$,
当且仅当t=$\frac{1}{t}$,即m=0时,${S}_{AB{F}_{1}}$取得最大值,
∴△ABF1面积最大值为$\sqrt{2}$,
则rmax=$\frac{1}{2}$,
∴△ABF1的内切圆的面积最大值为$\frac{π}{4}$,此时直线l的方程为x=1.…15分
点评 本题主要考查,直线、圆、圆锥曲线的方程,直线与椭圆的位置关系等基本知识,同时考查解析几何的基本思想方法和综合解题能力,考查计算能力,属于中档题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:填空题
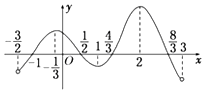 已知函数y=f(x)在定义域(-$\frac{3}{2}$,3)内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].
已知函数y=f(x)在定义域(-$\frac{3}{2}$,3)内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是奇函数 | B. | π为f(x)的最小正周期 | ||
| C. | f(x)的对称轴方程为x=kπ(k∈Z) | D. | f(x)的值域为[cos1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
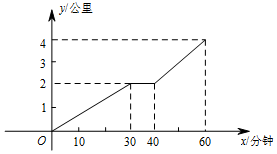 从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题:
从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com