
设双曲线 -
- =1的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
=1的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
(A) (B)5 (C)
(B)5 (C)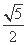 (D)
(D)
科目:高中数学 来源: 题型:
设双曲线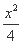 -
-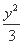 =1的左、右焦点分别为F1,F2,过F1的直线l交双曲线左支于A、B两点,则|BF2|+|AF2|的最小值为( )
=1的左、右焦点分别为F1,F2,过F1的直线l交双曲线左支于A、B两点,则|BF2|+|AF2|的最小值为( )
(A)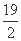 (B)11 (C)12 (D)16
(B)11 (C)12 (D)16
查看答案和解析>>
科目:高中数学 来源: 题型:
定义:关于x的不等式|x-A|<B的解集叫A的B邻域.
已知a+b-2的a+b邻域为区间(-2,8),其中a、b分别为椭圆 +
+ =1的长半轴长和短半轴长,若此椭圆的一焦点与抛物线y2=4
=1的长半轴长和短半轴长,若此椭圆的一焦点与抛物线y2=4 x的焦点重合,则椭圆的方程为( )
x的焦点重合,则椭圆的方程为( )
(A)  +
+ =1 (B)
=1 (B) 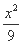 +
+ =1
=1
(C) 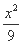 +
+ =1 (D)
=1 (D)  +
+ =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A、B两点,|AB|=4 ,则C的实轴长为( )
,则C的实轴长为( )
(A) (B)2
(B)2 (C)4 (D)8
(C)4 (D)8
查看答案和解析>>
科目:高中数学 来源: 题型:
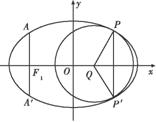
如图,椭圆的中心为原点O,长轴在x轴上,离心率e=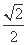 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
,过左焦点F1作x轴的垂线交椭圆于A、A′两点, 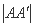 =4.
=4.
(1)求该椭圆的标准方程;
(2)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP′Q的面积S的最大值,并写出对应的圆Q的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆 +
+ =1(a>b>0)与抛物线y2=2px(p>0)有相同的焦点,P、Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆
=1(a>b>0)与抛物线y2=2px(p>0)有相同的焦点,P、Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆 +
+ =1(a>b>0)的离心率为 .
=1(a>b>0)的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系数抽样三种方案.使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有如下四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270.
关于上述样本的下列结论中,正确的是( )
A.②③都不能为系统抽样 B.②④都不能为分层抽样
C.①④都可能为系统抽样 D.①③都可能为分层抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
一只袋子中装有7个红玻璃球,3个绿玻璃球,从中无放回地任意抽取两次,每次只取一个,取得两个红球的概率为 ,取得两个绿球的概率为
,取得两个绿球的概率为 ,则取得两个同颜色的球的概率为________;至少取得一个红球的概率为________.
,则取得两个同颜色的球的概率为________;至少取得一个红球的概率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com