
 在如图所示的锐角三角形空地中,欲建立一个内接矩形花园(阴影部分),则其边长为x(单位:m),设花园面积为S,
在如图所示的锐角三角形空地中,欲建立一个内接矩形花园(阴影部分),则其边长为x(单位:m),设花园面积为S,分析 (Ⅰ)根据△ADE∽△ABC可得y与x的关系,然后将y用x表示,根据矩形的面积公式可得函数s(x) 的解析式;
(Ⅱ)先对二次函数进行配方,然后根据二次函数的性质可知开口向下的二次函数在对称轴处取最大值,从而求出所求;
(Ⅲ)欲建一个面积不小于300m2的内接矩形花园,可得不等式,即可求其边长x的取值范围.
解答 解:(Ⅰ)如图∵△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AD}{AB}=\frac{AB-BD}{AB}$,
设矩形的另一边长为y, ∴$\frac{x}{40}=\frac{40-y}{40}$,
∴$\frac{x}{40}=\frac{40-y}{40}$,
∴y=40-x(0<x<40),
∴S(x)=x(40-x)=40x-x2,定义域为:(0,40);
(Ⅱ)S(x)=40x-x2=-(x-20)2+400,0<x<40,
∴x=20时,函数S(x)最大值400m2.
(Ⅲ)欲建一个面积不小于300m2的内接矩形花园,则40x-x2≥300,
∴(x-10)(x-30)≤0,∴10≤x≤30.
点评 本题主要考查了三角形相似的应用,以及二次函数求最值,同时考查了分析问题的能力和运算求解的能力,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | ±9 | B. | 9 | C. | 3 | D. | ±3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1或x>$\frac{1}{4}$} | B. | R | C. | {x|-$\frac{1}{3}$<x<$\frac{3}{2}$} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
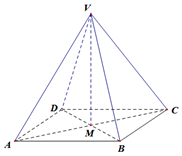 如图,已知正四棱锥V-ABCD中,AC与BD交于点M,VM是棱锥的高,若AC=6cm,VC=5cm.
如图,已知正四棱锥V-ABCD中,AC与BD交于点M,VM是棱锥的高,若AC=6cm,VC=5cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com