
在△ABC中,角A,B,C的对边分别为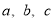 ,且A,B,C成等差数列。
,且A,B,C成等差数列。
(1)若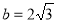 ,
,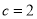 ,求△ABC的面积;
,求△ABC的面积;
(2)若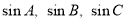 成等比数列,试判断△ABC的形状。
成等比数列,试判断△ABC的形状。
(1)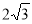 ;(2)等边三角形
;(2)等边三角形
【解析】
试题分析:(1)由A,B,C成等差数列得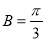 , 又
, 又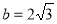 ,
,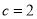 ,法一:由正弦定理得
,法一:由正弦定理得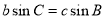 ,所以
,所以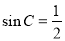 , 又
, 又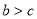 ,所以
,所以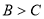 ,即C为锐角,所以
,即C为锐角,所以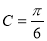 ,从而
,从而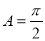 , 所以
, 所以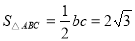 .法二:由余弦定理得
.法二:由余弦定理得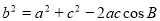 ,即
,即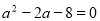 ,得
,得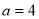 .所以
.所以
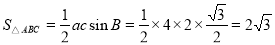
(2)由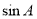 ,
,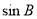 ,
,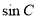 成等比数列,所以
成等比数列,所以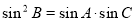 ,由正弦定理得
,由正弦定理得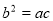 由余弦定理得
由余弦定理得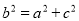
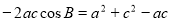 , 所以
, 所以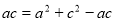 ,即
,即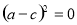 ,即
,即 .又因为
.又因为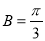 ,所以△ABC为等边三角形。
,所以△ABC为等边三角形。
试题解析:因为A,B,C成等差数列,所以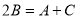 。又A+B+C=
。又A+B+C=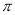 ,所以
,所以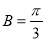 。
。
(1)解法一:因为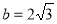 ,
,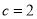 ,所以
,所以
由正弦定理得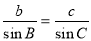 ,即
,即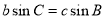 ,即
,即 ,
,
得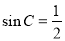 。
。
因为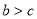 ,所以
,所以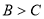 ,即C为锐角,所以
,即C为锐角,所以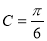 ,从而
,从而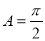 。
。
所以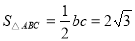 。
。
解法二:由余弦定理得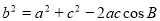 ,
,
即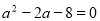 ,得
,得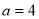 。
。
所以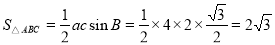 。
。
(2)因为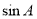 ,
,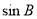 ,
,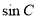 成等比数列,所以
成等比数列,所以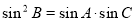 。
。
由正弦定理得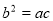
由余弦定理得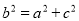
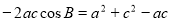 。
。
所以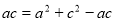 ,即
,即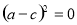 ,即
,即 。
。
又因为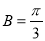 ,所以△ABC为等边三角形。
,所以△ABC为等边三角形。
考点:正弦定理与余弦定理以及等差、等比数列的性质


科目:高中数学 来源:2016届江苏省高一下学期期中考试数学试卷(解析版) 题型:填空题
已知 △ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x-y-5=0,AC边上的高BH所在的直线方程为x-2y-5=0,则顶点C的坐标为 .
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高一下学期期末考试数学试卷(解析版) 题型:填空题
为了了解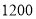 名学生对学校某项教改试验的意见,打算从中抽取一个容量为
名学生对学校某项教改试验的意见,打算从中抽取一个容量为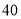 的样考虑用系统抽样,则分段的间隔
的样考虑用系统抽样,则分段的间隔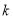 为_______________.
为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com