
【题目】在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且满足
,且满足![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)若![]() ,
,![]() ,线段
,线段![]() 的中垂线交
的中垂线交![]() 于点
于点![]() ,求线段
,求线段![]() 的长.
的长.
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() .
.
(1)若抛物线![]() 的焦点到准线的距离为4,直线
的焦点到准线的距离为4,直线![]() ,求直线
,求直线![]() 截抛物线
截抛物线![]() 所得的弦长;
所得的弦长;
(2)过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,过点
两点,过点![]() 作抛物线的切线,两切线相交于点
作抛物线的切线,两切线相交于点![]() ,若
,若![]() 分别表示直线
分别表示直线![]() 与直线
与直线![]() 的斜率,且
的斜率,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程及直线
的方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为3,中位数为4 B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3 D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了了解2018年当地居民网购消费情况,随机抽取了100人,对其2018年全年网购消费金额(单位:千元)进行了统计,所统计的金额均在区间![]() 内,并按
内,并按![]() ,
,![]() ,…,
,…,![]() 6组,制成如图所示的频率分布直方图.
6组,制成如图所示的频率分布直方图.
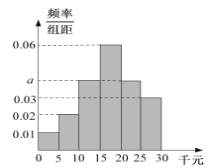
(1)求图中![]() 的值;
的值;
(2)若将全年网购消费金额在20千元及以上者称为网购迷.结合图表数据,补全![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为样本数据中的网购迷与性别有关系?说明理由;
的把握认为样本数据中的网购迷与性别有关系?说明理由;
男 | 女 | 合计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
合计 |
下面的临界值表仅供参考:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
附:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地4个蔬菜大棚顶部,阳光照在一棵棵茁壮生长的蔬菜上,这些采用水培、无土栽培方式种植的各类蔬菜,成为该地区居民争相购买的对象,过去50周的资料显示,该地周光照量![]() (小时)都在30以上,其中不足50的周数大约5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周,根据统计某种改良黄瓜每个蔬菜大棚增加量
(小时)都在30以上,其中不足50的周数大约5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周,根据统计某种改良黄瓜每个蔬菜大棚增加量![]() (百斤)与每个蔬菜大棚使用农夫1号液体肥料
(百斤)与每个蔬菜大棚使用农夫1号液体肥料![]() (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.
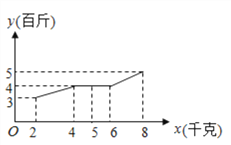
(1)依据数据的折线图,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大鹏增加量
;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大鹏增加量![]() 是多少斤?
是多少斤?
(2)因蔬菜大棚对光照要求较大,某光照控制仪商家为应对恶劣天气对光照的影响,为该基地提供了部分光照控制仪,该商家希望安装的光照控制仪尽可能运行,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 | 30<X<50 |
|
|
光照控制仪最多可运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照仪周利润为4000元;若某台光照仪未运行,则该台光照仪周亏损500元,欲使商家周总利润的均值达到最大,应安装光照控制仪多少台?
附:回归方程系数公式: 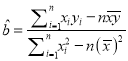 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com