
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 的平分线,且
的平分线,且![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
由三角形内角平分线的性质可得,BD![]() BC,CD
BC,CD![]() BC;在△ABD和△ACD中,分别利用余弦定理可得
BC;在△ABD和△ACD中,分别利用余弦定理可得![]() cos∠1;由于 ∠1∈(0,
cos∠1;由于 ∠1∈(0,![]() ),由此解得k的取值范围.
),由此解得k的取值范围.
如图所示,
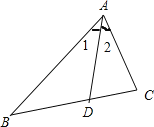
∵在△ABC中,AD是∠A的平分线,AB=2AC,
∴![]() 2,∠1=∠2.
2,∠1=∠2.
令AC=a,DC=b,AD=c,则AB=2a,BD=2b.
在△ABD与△ACD中,分别利用余弦定理可得:
BD2=AB2+AD2﹣2ABADcos∠1,
DC2=AC2+AD2﹣2ACADcos∠2,
∴4b2=4a2+c2﹣4accos∠1,b2=a2+c2﹣2accos∠2,
化为3c2﹣4accos∠1=0,又a=tc,
∴![]() cos∠1,
cos∠1,
∵∠1∈(0,![]() ),∴cos∠1∈(0,1).
),∴cos∠1∈(0,1).
∴![]() ∈(0,
∈(0,![]() ),即
),即![]()
故选:A


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知![]() 与
与![]() 分别是边长为1与2的正三角形,
分别是边长为1与2的正三角形, ![]() ,四边形
,四边形![]() 为直角梯形,且
为直角梯形,且![]() ,
, ![]() ,点
,点![]() 为
为![]() 的重心,
的重心, ![]() 为
为![]() 中点,
中点, ![]() 平面
平面![]() ,
, ![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的三等分点.
的三等分点.
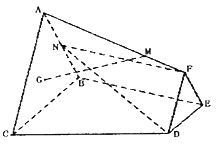
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的余弦值为
的余弦值为![]() ,试求异面直线
,试求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 满足
满足![]() .
.
(Ⅰ)当![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅱ)若关于x的方程![]() 的解集中有且只有一个元素,求a的值;
的解集中有且只有一个元素,求a的值;
(Ⅲ)设![]() ,若对
,若对![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求a的取值范围.
上的最大值与最小值的差不超过1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.

(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有一名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() =2px经过点
=2px经过点![]() (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com