
| A. | (0,1) | B. | $[\sqrt{3}-1,1)$ | C. | $(0,\sqrt{3}-1]$ | D. | $[-\sqrt{3}-1,\sqrt{3}-1]$ |
分析 化标准方程易得圆的圆心为M(a,a),半径r=$\sqrt{2}$|a|,由题意可得1≥$\frac{PC}{AC}$≥sin∠CAP,由距离公式可得a的不等式,解不等式可得.
解答 解:化圆的方程为标准方程可得(x-a)2+(y-a)2=2a2,
∴圆的圆心为C(a,a),半径r=$\sqrt{2}$|a|,
∴AC=$\sqrt{{a}^{2}+(a-2)^{2}}$,PC=$\sqrt{2}$|a|,
∵AC和PC长度固定,
∴当P为切点时,∠CAP最大,
∵圆C上存在点P使得∠CAP=45°,
∴若最大角度大于45°,则圆C上存在点P使得∠CAP=45°,
∴$\frac{PC}{AC}$=$\frac{\sqrt{2}|a|}{\sqrt{{a}^{2}+(a-2)^{2}}}$≥sin∠CAP=sin45°=$\frac{\sqrt{2}}{2}$,
整理可得a2+2a-2≥0,解得a≥$\sqrt{3}-1$或a≤-$\sqrt{3}-1$,
又$\frac{PC}{AC}$=$\frac{\sqrt{2}|a|}{\sqrt{{a}^{2}+(a-2)^{2}}}$≤1,解得a≤1,
又点 A(0,2)为圆C:x2+y2-2ax-2ay=0外一点,
∴02+22-4a>0,解得a<1
∵a>0,∴综上可得$\sqrt{3}$-1≤a<1.
故选B.
点评 本题考查圆的一般式方程和圆的性质,涉及距离公式的应用,属中档题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
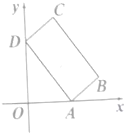 如图所示,矩形ABCD的顶点A,D分别在x轴,y轴正半轴(含坐标原点)滑动,其中AD=4,AB=2.
如图所示,矩形ABCD的顶点A,D分别在x轴,y轴正半轴(含坐标原点)滑动,其中AD=4,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{{e}^{2}}$ | B. | ln3-2 | C. | $\frac{3}{e}$-1 | D. | 3e-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com