
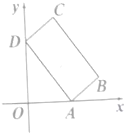
 如图所示,矩形ABCD的顶点A,D分别在x轴,y轴正半轴(含坐标原点)滑动,其中AD=4,AB=2.
如图所示,矩形ABCD的顶点A,D分别在x轴,y轴正半轴(含坐标原点)滑动,其中AD=4,AB=2.分析 (1)$∠DAO=\frac{π}{4}$时,容易求出点C,D的坐标,从而求出向量$\overrightarrow{OC}+\overrightarrow{OD}$的坐标,进而求出其长度
(2)可设∠DAO=θ,并过点B作BM⊥AO,过点C作CN⊥OD,垂足分别为M,N,可以求出点B,C的坐标,进行向量数量积的坐标运算求出$\overrightarrow{OB}•\overrightarrow{OC}=12sinθcosθ+12si{n}^{2}θ$,根据二倍角的正余弦公式,两角差的正弦公式化简得到$\overrightarrow{OB}•\overrightarrow{OC}=6\sqrt{2}sin(2θ-\frac{π}{4})+6$,根据θ的范围即可求出该数量积的最大值.
解答 解:(1)若$∠DAO=\frac{π}{4}$,则可得:$C(\sqrt{2},3\sqrt{2}),D(0,2\sqrt{2})$;
∴$|{\overrightarrow{OC}+\overrightarrow{OD}}|=|{(\sqrt{2},5\sqrt{2})}|=2\sqrt{13}$;
(2)如图,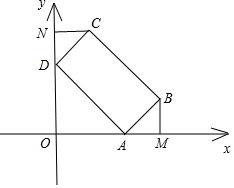
过点B作BM⊥AO,垂足为M,过点C作CN⊥OD,垂足为N,设∠DAO=θ,
则∠CDN=θ,∠ABM=θ;z∴$2θ-\frac{π}{4}=\frac{π}{2}$z
∴点B(4cosθ+2sinθ,2sinθ),C(2sinθ,4sinθ+2cosθ);
则$\overrightarrow{OB}•\overrightarrow{OC}=8sinθcosθ+4si{n}^{2}θ$+8sin2θ+4sinθcosθ
=12sinθcosθ+12sin2θ
=6sin2θ+6(1-cos2θ)
=$6\sqrt{2}sin(2θ-\frac{π}{4})+6$;
∵$θ∈[0,\frac{π}{2}]$;
∴$(2θ-\frac{π}{4})∈[-\frac{π}{4},\frac{3π}{4}]$;
∴$2θ-\frac{π}{4}=\frac{π}{2}$时,$\overrightarrow{OB}•\overrightarrow{OC}$取最大值$6\sqrt{2}+6$.
点评 考查平面上点的坐标的求法,根据点的坐标得出向量坐标,向量坐标的加法和数量积运算,根据向量坐标能求向量长度,以及二倍角的正余弦公式,两角差的正弦公式,熟悉正弦函数的最值.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},3)$ | B. | $(-2,\frac{1}{2})$ | C. | (-2,3) | D. | $(\frac{1}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [18,24] | B. | [16,24] | C. | (16,36) | D. | (24,36) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或1 | B. | 0 | C. | 0或2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x+2=0} | B. | {x|x2+1=0,x∈R} | C. | {x|x<1} | D. | {(x,y)|y2=-x2,x,y∈R} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | $[\sqrt{3}-1,1)$ | C. | $(0,\sqrt{3}-1]$ | D. | $[-\sqrt{3}-1,\sqrt{3}-1]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{6}$-$\sqrt{2}$ | C. | $\sqrt{3}+\sqrt{2}$ | D. | 2+$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com