
| A. | [18,24] | B. | [16,24] | C. | (16,36) | D. | (24,36) |
分析 通过建立直角坐标系求出AB所在直线的方程,设出M,N的坐标,将$\overrightarrow{CM}$•$\overrightarrow{CN}$=2(b-2)2+16,0≤b≤4,求出范围即可.
解答 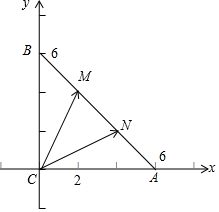 解:RT△ABC中,∠BCA=90°,AC=BC=6,M、N是斜边AB上的动点,MN=2$\sqrt{2}$,
解:RT△ABC中,∠BCA=90°,AC=BC=6,M、N是斜边AB上的动点,MN=2$\sqrt{2}$,
以C为坐标原点,CA为x轴建立平面坐标系,
则A(6,0),B(0,6),
∴AB所在直线的方程为:$\frac{x}{6}$+$\frac{y}{6}$=1,即y=6-x.
设N(a,6-a),M(b,6-b),且0≤a≤6,0≤b≤6,不妨设a>b,
∵MN=2$\sqrt{2}$,∴(a-b)2+(b-a)2=8,∴a-b=2,
∴a=b+2,∴0≤b≤4,
则$\overrightarrow{CM}$•$\overrightarrow{CN}$═(a,6-a)•(b,6-b)=2ab-6(a+b)+36
=2(b2-4b+12)=2(b-2)2+16,0≤b≤4,
∴当b=0或b=4时有最大值24;当b=2时有最小值16.
的取值范围为[16,24],
故选:B.
点评 本题主要考查两个向量的数量积的运算,熟练掌握通过建立直角坐标系、数量积的坐标运算是解题的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$倍 | B. | 2倍 | C. | $\frac{\sqrt{2}}{4}$倍 | D. | $\sqrt{2}$倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
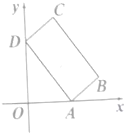 如图所示,矩形ABCD的顶点A,D分别在x轴,y轴正半轴(含坐标原点)滑动,其中AD=4,AB=2.
如图所示,矩形ABCD的顶点A,D分别在x轴,y轴正半轴(含坐标原点)滑动,其中AD=4,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com