
| A. | {x|-1<x<0或x<-1} | B. | {x|-1<x<0或x>1} | C. | {x|x<-1或0<x<1} | D. | {x|-1<x<0或0<x<1} |
分析 根据题意,令g(x)=$\frac{f(x)}{{e}^{x}}$,对其求导,结合题意分析可得在(0,+∞)函数g(x)为减函数,且g(1)=$\frac{f(1)}{{e}^{1}}$=0,分析可得当x>1时,有g(x)=$\frac{f(x)}{{e}^{x}}$<0,则有f(x)<0;当0<x<1时,有g(x)=$\frac{f(x)}{{e}^{x}}$>0,则有f(x)>0;进而结合函数f(x)的奇偶性,可得f(x)在(-∞,0)上的符号情况,由此可得ln|x|f(x)>0?$\left\{\begin{array}{l}{ln|x|<0}\\{x>1}\end{array}\right.$或$\left\{\begin{array}{l}{ln|x|>0}\\{0<x<1}\end{array}\right.$或$\left\{\begin{array}{l}{ln|x|>0}\\{x<-1}\end{array}\right.$或$\left\{\begin{array}{l}{ln|x|<0}\\{-1<x<0}\end{array}\right.$,解可得不等式的解集,即可得答案.
解答 解:根据题意,令g(x)=$\frac{f(x)}{{e}^{x}}$,则其导数且g′(x)=$\frac{f(x)}{{e}^{x}}$=$\frac{f′(x)•{e}^{x}-f(x)•{e}^{x}}{{(e}^{x})^{2}}$=$\frac{f′(x)-f(x)}{{e}^{x}}$,
又由当x>0时,f′(x)-f(x)<0恒成立,
则有g′(x)=$\frac{f(x)}{{e}^{x}}$=$\frac{f′(x)•{e}^{x}-f(x)•{e}^{x}}{{(e}^{x})^{2}}$=$\frac{f′(x)-f(x)}{{e}^{x}}$<0,
即在(0,+∞)函数g(x)为减函数;
又由f(1)=0,则g(1)=$\frac{f(1)}{{e}^{1}}$=0,
则当x>1时,有g(x)=$\frac{f(x)}{{e}^{x}}$<0,则有f(x)<0;
当0<x<1时,有g(x)=$\frac{f(x)}{{e}^{x}}$>0,则有f(x)>0;
又由函数f(x)是定义在R上的奇函数,
则当x<-1时,有f(x)>0;
当-1<x<0时,有f(x)<0;
对于不等式ln|x|f(x)>0,
则有$\left\{\begin{array}{l}{ln|x|<0}\\{x>1}\end{array}\right.$或$\left\{\begin{array}{l}{ln|x|>0}\\{0<x<1}\end{array}\right.$或$\left\{\begin{array}{l}{ln|x|>0}\\{x<-1}\end{array}\right.$或$\left\{\begin{array}{l}{ln|x|<0}\\{-1<x<0}\end{array}\right.$,
解可得x<-1或0<x<1,
即不等式ln|x|f(x)>0的解集为{x<-1或0<x<1},
故选:C.
点评 本题考查函数的导数与函数单调性的关系,涉及函数的奇偶性的性质,构造函数g(x)是解答本题的关键.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+1≥0 | B. | ?x0∈R,x${\;}_{0}^{2}$+1>0 | ||
| C. | ?x∈R,x2+1>0 | D. | ?x0∈R,x${\;}_{0}^{2}$+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:解答题
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 过点
过点 ,直线
,直线 交
交 轴于
轴于 ,且
,且 ,
,  为坐标原点.
为坐标原点.
(1)求椭圆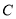 的方程;
的方程;
(2)设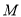 是椭圆
是椭圆 的上顶点,过点
的上顶点,过点 分别作直线
分别作直线 交椭圆
交椭圆 于
于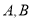 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三10月月考数学(文)试卷(解析版) 题型:解答题
已知椭圆 的两个焦点为
的两个焦点为 ,椭圆上一点
,椭圆上一点 满足
满足 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线 与椭圆有不同交点
与椭圆有不同交点 ,且
,且 (
( 为坐标原点),求实数
为坐标原点),求实数 的取
的取
值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com