
分析 (1)利用绝对值三角不等式、基本不等式,证得f(x)≥8成立;
(2)利用绝对值三角不等式可得f(1)≥$\frac{16}{m}$+m,再根据$\frac{16}{m}$+m>17,解一元二次不等式,求得实数m的取值范围,综合可得结论.
解答 解:(1)证明:∵函数f(x)=$|{x+\frac{16}{m}}|+|{x-m}$|
≥|x+$\frac{16}{m}$-(x-m)|=|$\frac{16}{m}$+m|=|$\frac{16}{m}$|+|m|≥2$\sqrt{16}$=8,
∴f(x)≥8成立.
(2)∵m>0,且f(1)=|1+$\frac{16}{m}$|+|1-m|≥|1+$\frac{16}{m}$-(1-m)|=|$\frac{16}{m}$+m|=$\frac{16}{m}$+m>17,
∴m2-17m+16>0,即(m-16)•(m-1)>0,由此求得m>16,或 m<1,
故实数m的取值范围为{m|m>16,或 0<m<1}.
点评 本题主要考查绝对值三角不等式、基本不等式的应用,一元二次不等式的解法,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | -2 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (-1,+∞) | C. | [-1,0) | D. | (-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<0或x<-1} | B. | {x|-1<x<0或x>1} | C. | {x|x<-1或0<x<1} | D. | {x|-1<x<0或0<x<1} |
查看答案和解析>>
科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:解答题
在一次篮球定点投篮训练中,规定每人最多投 次,在
次,在 处每投进一球得
处每投进一球得 分; 在
分; 在 处每投进一球得
处每投进一球得 分,如果前两次得分之和超过
分,如果前两次得分之和超过 分就停止投篮 ; 否則投第三次 , 某向学在
分就停止投篮 ; 否則投第三次 , 某向学在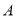 处的投中率,
处的投中率, ,在
,在 处的投中率为
处的投中率为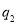 ,该同学选择先在
,该同学选择先在 处投一球,以后都在
处投一球,以后都在 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求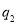 的值;
的值;
(2)求随机变量 的数学期望;
的数学期望;
(3)试比较该同学选择上述方式投篮得分超过 分与选择都在
分与选择都在 处投篮得分超过
处投篮得分超过 分的概率的大小.
分的概率的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com