
分析 (Ⅰ)当a=1时,f(x)=x-ex,f'(x)=1-ex.切线的斜率k=f'(0)=0,切点(0,f(0)),即可求得切线方程.
(Ⅱ)由f(x)=x-aex,得f'(x)=1-aex.分a≤0,a>求出函数f(x)的单调区间,结合图象求解.
解答 解:(Ⅰ)当a=1时,f(x)=x-ex,f'(x)=1-ex.
当x=0时,y=-1,又f'(0)=0,
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=-1.…(4分)
(Ⅱ)由f(x)=x-aex,得f'(x)=1-aex.
当a≤0时,f'(x)>0,此时f(x)在R上单调递增.
当x=a时,f(a)=a-aea=a(1-ea)≤0,当x=1时,f(1)=1-ae>0,
所以当a≤0时,曲线y=f(x)与x轴有且只有一个交点; …(8分)
当a>0时,令f'(x)=0,得x=-lna.f(x)与f'(x)在区间(-∞,+∞)上的情况如下:
| x | (-∞,-lna) | -lna | (-lna,+∞) |
| f'(x) | + | 0 | - |
| f(x) | ↗ | 极大值 | ↘ |
点评 本题考查了导数的综合应用,利用导数求切线方程,函数图象与横轴交点问题.属于中档题.


科目:高中数学 来源: 题型:解答题
 近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下表示.
近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下表示. | 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 0.100 | |
| 第2组 | [165,170) | ① | |
| 第3组 | [170,175) | 20 | ② |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | 3 | C. | 2$\sqrt{2}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
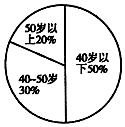 200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方式,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为23,第9组抽取号码为43;若采用分层抽样,40-50岁年龄段应抽取12人.
200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方式,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为23,第9组抽取号码为43;若采用分层抽样,40-50岁年龄段应抽取12人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -7 | C. | 12 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com