
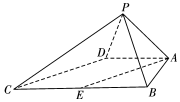
 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.分析 (1)证明四边形AECD是平行四边形得出AE∥CD,从而有AE∥平面PCD;
(2)连结DE,BD,设AE∩BD=O,由三线合一证明OP⊥BD,根据勾股定理逆定理证明OP⊥OA,故而OP⊥平面ABCD,于是VP-ABCD=$\frac{1}{3}{S}_{梯形ABCD}•OP$.
解答 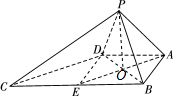 (1)证明:∵∠ABC=∠BAD=90°,
(1)证明:∵∠ABC=∠BAD=90°,
∴AD∥BC,
∵BC=2AD,E是BC的中点,
∴AD=CE,
∴四边形ADCE是平行四边形,
∴AE∥CD,
又AE?平面PCD,CD?平面PCD,
∴AE∥平面PCD.
(2)解:连结DE,BD,设AE∩BD=O,
则四边形ABED是正方形,
∴O为BD的中点,
∵△PAB与△PAD都是边长为2的等边三角形,
∴BD=2$\sqrt{2}$,OB=$\sqrt{2}$,OA=$\sqrt{2}$,PA=PB=2,
∴OP⊥OB,OP=$\sqrt{2}$,
∴OP2+OA2=PA2,即OP⊥OA,
又OA?平面ABCD,BD?平面ABCD,OA∩BD=O,
∴OP⊥平面ABCD.
∴VP-ABCD=$\frac{1}{3}{S}_{梯形ABCD}•OP$=$\frac{1}{3}×\frac{1}{2}(2+4)×2×\sqrt{2}$=2$\sqrt{2}$.
点评 本题考查了线面平行的判定,线面垂直的判定,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{3}{2}i$ | D. | $\frac{3}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
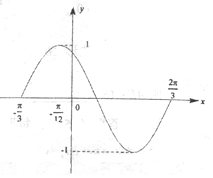 如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{3}$,$\frac{2π}{3}$]上的图象,为了得到这个函数的图象.只需将y=cosx(x∈R)的图象上的所有点( )
如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{3}$,$\frac{2π}{3}$]上的图象,为了得到这个函数的图象.只需将y=cosx(x∈R)的图象上的所有点( )| A. | 向左平移$\frac{π}{6}$个单位长度,再把所有点的横坐标扩大到原来的2倍 | |
| B. | 向左平移$\frac{π}{12}$个单位长度.再把所有点的横坐标扩大到原来的2倍 | |
| C. | 把所有点的横坐标缩短到原来的$\frac{1}{2}$,再向左平移$\frac{π}{12}$个单位长度 | |
| D. | 把所有点的横坐标缩短到原来的$\frac{1}{2}$,再向左平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com