
分析 (1)公比为m的等比数列{an}中,a3=2,a1+a2+a3=6.可得${a}_{1}{m}^{2}$=2,${a}_{1}(1+m+{m}^{2})$=6,解出即可得出.
(2)由(1)可得:an=2或an=$8×(-\frac{1}{2})^{n-1}$.利用错位相减法、等比数列的求和公式即可得出.
解答 解:(1)公比为m的等比数列{an}中,a3=2,a1+a2+a3=6.
∴${a}_{1}{m}^{2}$=2,${a}_{1}(1+m+{m}^{2})$=6,
解得m=1,a1=2或m=-$\frac{1}{2}$,a1=8.
∴m=1,或m=-$\frac{1}{2}$.
(2)由(1)可得:an=2或an=$8×(-\frac{1}{2})^{n-1}$.
①an=2时,nan=2n.
∴{nan}的前n项和Tn=$2×\frac{n(n+1)}{2}$=n2+n.
②an=$8×(-\frac{1}{2})^{n-1}$.nan=8n×$(-\frac{1}{2})^{n-1}$.
∴{nan}的前n项和Tn=8$[1+2×(-\frac{1}{2})+3×(-\frac{1}{2})^{2}$+…+$n×(-\frac{1}{2})^{n-1}]$,
∴$-\frac{1}{2}$Tn=8$[-\frac{1}{2}+2×(-\frac{1}{2})^{2}$+…+(n-1)×$(-\frac{1}{2})^{n-1}$+n×$(-\frac{1}{2})^{n}]$.
∴$\frac{3}{2}{T}_{n}$=8$[1+(-\frac{1}{2})+(-\frac{1}{2})^{2}$+…+$(-\frac{1}{2})^{n-1}-$n×$(-\frac{1}{2})^{n}]$.
∴Tn=$\frac{32}{9}$-$\frac{32+48n}{9}$×$(-\frac{1}{2})^{n}$.
点评 本题考查了错位相减法、等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在$({0,\frac{π}{3}})$上单调递增 | B. | 图象关于直线$x=\frac{π}{6}$对称 | ||
| C. | $f({\frac{π}{3}})=\frac{{\sqrt{3}}}{2}$ | D. | 当$x=\frac{5π}{12}$时有最小值-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
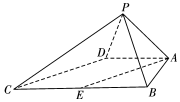 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | {1,3} | C. | {-1,1,3} | D. | {-3,-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
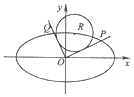 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,直线y=1与椭圆C的两交点间距离为8.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,直线y=1与椭圆C的两交点间距离为8.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:填空题
已知平面α,β和直线m,给出条件:①m∥α;②m⊥α;③m?α;④α∥β.当满足条件________时,有m⊥β.(填所选条件的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com