
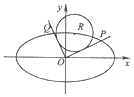
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,直线y=1与椭圆C的两交点间距离为8.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,直线y=1与椭圆C的两交点间距离为8.分析 (Ⅰ)由椭圆的离心率公式求得a2=4b2,由椭圆过点(4,1),代入椭圆方程,即可求得a和b的值,求得椭圆方程;
(Ⅱ)利用点到直线距离公式(x02-4)k12-2x0y0k1+(y02-4)=0,同理求得:(x02-4)k22-2x0y0k2+(y02-4)=0,则k1,k2是方程(x02-4)k2-2x0y0k+(y02-4)=0的两个不相等的实根,根据韦达定理即可求得k1•k2为定值;
(Ⅲ)将直线OP和OQ的方程,代入椭圆方程,即可求得P和Q点坐标,根据两点之间的距离公式|OP|2+|OQ|2=x12+y12+x22+y22,由k1•k2=-$\frac{1}{4}$,即可求得|OP|2+|OQ|2为定值.
解答 解:(Ⅰ)由椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,则a2=4b2,
由直线过点(4,1),代入$\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,解得:b2=5,则a2=20,
∴椭圆的标准方程:$\frac{{x}^{2}}{20}+\frac{{y}^{2}}{5}=1$;
(Ⅱ)证明:由直线OP:y=k1x,直线OQ:y=k2x,
由直线OP为圆R的切线,
$\frac{丨{k}_{1}{x}_{0}-{y}_{0}丨}{\sqrt{{k}_{1}^{2}+1}}$=2,(x02-4)k12-2x0y0k1+(y02-4)=0,
同理可得:(x02-4)k22-2x0y0k2+(y02-4)=0,
∴k1,k2是方程(x02-4)k2-2x0y0k+(y02-4)=0的两个不相等的实根,
由x02-4≠0,△>0,
则k1•k2=$\frac{{y}_{0}^{2}-4}{{x}_{0}^{2}-4}$,
由R(x0,y0)在椭圆上,即y02=5-$\frac{1}{4}$x02,
∴k1•k2=$\frac{{y}_{0}^{2}-4}{{x}_{0}^{2}-4}$=$\frac{1-\frac{1}{4}{x}_{0}^{2}}{{x}_{0}^{2}-4}$=-$\frac{1}{4}$,
∴k1•k2为定值-$\frac{1}{4}$;
(Ⅲ)经判断|OP|2+|OQ|2为定值,
(i)由直线OP,OQ不落在坐标轴上时,设P(x1,y1),Q(x2,y2),
联立$\left\{\begin{array}{l}{y={k}_{1}x}\\{\frac{{x}^{2}}{20}+\frac{{y}^{2}}{5}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}_{1}^{2}=\frac{20}{1+4{k}_{1}^{2}}}\\{{y}_{1}^{2}=\frac{20{k}_{1}^{2}}{1+4{k}_{1}^{2}}}\end{array}\right.$,
∴x12+y12=$\frac{20(1+{k}_{1}^{2})}{1+4{k}_{1}^{2}}$,
同理,得x22+y22=$\frac{20(1+{k}_{2}^{2})}{1+4{k}_{2}^{2}}$,…13分
由k1•k2=-$\frac{1}{4}$,
得|OP|2+|OQ|2=x12+y12+x22+y22=$\frac{20(1+{k}_{1}^{2})}{1+4{k}_{1}^{2}}$+$\frac{20(1+{k}_{2}^{2})}{1+4{k}_{2}^{2}}$,
=$\frac{20(1+{k}_{1}^{2})}{1+4{k}_{1}^{2}}$+$\frac{20(1+\frac{1}{16{k}_{1}^{2}})}{1+\frac{1}{4{k}_{1}^{2}}}$,
=$\frac{20(1+{k}_{1}^{2})}{1+4{k}_{1}^{2}}$+$\frac{20(4{k}_{1}^{2}+\frac{1}{4})}{4{k}_{1}^{2}+1}$,
=$\frac{25+100{k}_{1}^{2}}{1+4{k}_{1}^{2}}$=25,
∴丨OP丨2+丨OQ丨2为定值,定值为25.
点评 本题考查了椭圆的定义标准方程、直线与圆相切的性质、一元二次方程的根与系数的关系,考查了分类讨论方法、推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{3}{2}i$ | D. | $\frac{3}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
已知点A(2,﹣3)、B(﹣3,﹣2)直线l过点P(1, 1),且与线段AB相交,则直线l的斜率k的取值范围是( )
A. 或k≤﹣4
或k≤﹣4
B. 或
或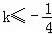
C.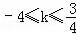
D.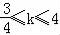
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com