
分析 设A(0,1),求出圆心C的坐标为(1,2),从而得到AC的斜率.由圆的性质,得当直线被圆截得弦长最短时,直线与经过A点的直径垂直,由此算出直线的斜率,即可得到所求直线的方程.
解答 解:∵圆(x-1)2+y2=4的圆心为C(1,0),
∴设A(0,1),得AC的斜率kAC=$\frac{0-1}{1-0}$=-1,
∵直线l经过点A(0,1),且l被圆(x-1)2+y2=4截得的弦长最短
∴直线l与经过点A(0,1)的直径垂直的直线
由此可得,直线l的斜率为k=-$\frac{1}{{k}_{AC}}$=1,
因此,直线l方程为y-1=x-0,即x-y+1=0
故答案为:x-y+1=0.
点评 本题考查直线的方程,着重考查了直线的基本量与方程、圆的方程和直线与圆的位置关系及两条直线垂直的充要条件等知识,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 91种 | B. | 90种 | C. | 89种 | D. | 86种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | $(\frac{π}{3},0)$ | C. | $(\frac{π}{6},0)$ | D. | $(\frac{π}{9},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
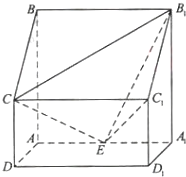 如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-5)2+(y-3)2=18 | B. | (x-5)2+(y-3)2=9 | C. | (x-3)2+(y-5)2=18 | D. | (x-3)2+(y-5)2=9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com