
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
分析 sinA+2sinBcosC=0,利用三角形内角和定理与诱导公式可得:sin(B+C)+2sinBcosC=0,展开化为:3sinBcosC+cosBsinC=0,cosC≠0,cosB≠0.因此3tanB=-tanC.可得:B为锐角,C为钝角.tanA=-tan(B+C)展开代入利用基本不等式的性质即可得出.
解答 解:∵sinA+2sinBcosC=0,∴sin(B+C)+2sinBcosC=0,
∴3sinBcosC+cosBsinC=0,cosC≠0,cosB≠0.
化为3tanB=-tanC.可得:B为锐角,C为钝角.
∴tanA=-tan(B+C)=-$\frac{tanB+tanC}{1-tanBtanC}$=$\frac{-(tanB-3tanB)}{1+3ta{n}^{2}B}$
=$\frac{2}{\frac{1}{tanB}+3tanB}$≤$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,当且仅当tanB=$\frac{\sqrt{3}}{3}$时取等号.
∴tanA的最大值是$\frac{\sqrt{3}}{3}$.
故选:A.
点评 本题考查了三角形内角和定理、诱导公式、和差公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}-\frac{1}{e}$ | B. | $-\frac{3}{2}-\frac{2}{e}$ | C. | $-\frac{3}{4}-\frac{1}{2e}$ | D. | $-1-\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为9尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为9尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( )| A. | 14斛 | B. | 28斛 | C. | 36斛 | D. | 66斛 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
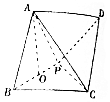 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,点A在平面PBC上的射影为PB的中点O,PB⊥AC.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,点A在平面PBC上的射影为PB的中点O,PB⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com