
分析 (1)根据极值的条件得出由$\left\{\begin{array}{l}{f(-1)=2}\\{{f}^{′}(-1)=0}\end{array}\right.$求解即可.
(2)求解$f'(x)=3{x^2}+4x+1=3(x+1)(x+\frac{1}{3})$,令f'(x)=0得:x=-1或$x=-\frac{1}{3}$,列表判断极值.
(3)根据f(-1)=2为极大值,必须$\left\{\begin{array}{l}{a>0}\\{\frac{a-2}{3a}>-1}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{\frac{a-2}{3a}<-1}\end{array}\right.$,求解不等式即可.
解答 解:(1)f'(x)=3ax2+2bx+c,由$\left\{\begin{array}{l}{f(-1)=2}\\{{f}^{′}(-1)=0}\end{array}\right.$解得:b=a+1,c=2-a,
(2)当a=1时,b=2,c=1
∴f(x)=x3+2x2+x+2
$f'(x)=3{x^2}+4x+1=3(x+1)(x+\frac{1}{3})$
令f'(x)=0得:x=-1或$x=-\frac{1}{3}$,列表如下:
| x | (-∞,-1) | -1 | ($-1,-\frac{1}{3}$) | $-\frac{1}{3}$ | ($-\frac{1}{3},+∞$) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
点评 本题综合考查了导数在解决极值问题中的运用,结合不等式,列表求解判断,属于考查综合能力的题目.


科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|x≤-2} | C. | {x|x<3} | D. | {x|-2≤x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a4•a6=25 | B. | a4•a6≤25 | C. | a4•a6>25 | D. | a4•a6<25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
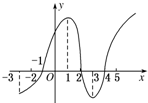 如图所示是y=f(x)的导数图象,则下列判断中正确结论的序号是②④.
如图所示是y=f(x)的导数图象,则下列判断中正确结论的序号是②④.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知定义在[0,1]上的函数y=f(x),f′(x)为f(x)的导函数,f(x)图象如图,对满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在[0,1]上的函数y=f(x),f′(x)为f(x)的导函数,f(x)图象如图,对满足0<x1<x2<1的任意x1,x2,给出下列结论:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com