
| 1 |
| 2n |
| n |
| 2n+1 |
| n+2 |
| 2n+1 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 22 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 23 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
| 1 |
| 22 |
| k |
| 2k+1 |
| 1 |
| 22 |
| 2 |
| 23 |
| k |
| 2k+1 |
| 1 |
| 2k+1 |
| 1 |
| 22 |
| 2 |
| 23 |
| k |
| 2k+1 |
| 1 |
| 2 |
| 1 |
| 23 |
| 2 |
| 24 |
| k |
| 2k+2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2k+1 |
| k |
| 2k+2 |
| ||||
1-
|
| k |
| 2k+2 |
| 1 |
| 2 |
| 2+k |
| 2k+2 |
| 2+k |
| 2k+1 |
| 1 |
| 2k+1 |
| 2+k |
| 2k+1 |
| k+1 |
| 2k+1 |
| k+1 |
| 2k+2 |
| n |
| 2n+1 |
| n |
| 2n+1 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 23 |
| 2 |
| 24 |
| 3 |
| 25 |
| n |
| 2n+2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n+1 |
| n |
| 2n+2 |
| ||||
1-
|
| n |
| 2n+2 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+2 |
| n+2 |
| 2n+1 |
| 3 |
| 22 |
| 4 |
| 23 |
| n+2 |
| 2n+1 |
| 1 |
| 2 |
| n |
| 2 |
| 3 |
| 23 |
| 4 |
| 24 |
| n+2 |
| 2n+2 |
| 1 |
| 2 |
| n |
| 2 |
| 3 |
| 4 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n+1 |
| n+2 |
| 2n+2 |
| n |
| 2 |
| 3 |
| 4 |
| ||||
1-
|
| n+2 |
| 2n+2 |
| n |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2n+1 |
| n+2 |
| 2n+2 |
| n |
| 2 |
| 1 |
| 2n+1 |
| n+2 |
| 2n+1 |
| n+4 |
| 2n+1 |


科目:高中数学 来源: 题型:
| A、(-1,2) |
| B、[-1,2) |
| C、(2,6) |
| D、[2,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:
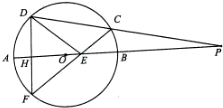 已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.
已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
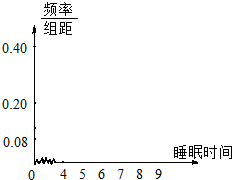 某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.
某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.| 序号(i) | 分组(睡眠时间) | 频数(人数) | 频率 | 频率/组距 |
| 1 | [4,5) | 0.12 | ||
| 2 | [5,6) | 10 | 0.20 | |
| 3 | [6,7) | s | ||
| 4 | [7,8) | t | ||
| 5 | [8,9) | 0.08 |
查看答案和解析>>
科目:高中数学 来源: 题型:
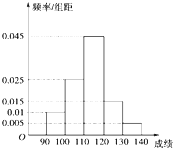 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com