
【题目】某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25 ![]() 米,为了便于游客休闲散步,该农庄决定在鱼塘内建三条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°.
米,为了便于游客休闲散步,该农庄决定在鱼塘内建三条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°. 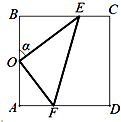
(1)设∠BOE=α,试将△OEF的周长l表示成α的函数关系式,并求出此函数的定义域;
(2)经核算,三条走廊每米建设费用均为4000元,试问如何设计才能使建设总费用最低并求出最低总费用.
【答案】
(1)解:∵在Rt△BOE中,OB=25,∠B=90°,∠BOE=α,
∴OE= ![]()
在Rt△AOF中,OA=25,∠A=90°,∠AFO=α,
∴OF= ![]() .
.
又∠EOF=90°,
∴EF= ![]() =
= ![]() ,
,
∴l=OE+OF+EF= ![]() .
.
当点F在点D时,这时角α最小,此时α= ![]() ;
;
当点E在C点时,这时角α最大,求得此时α= ![]() .
.
故此函数的定义域为[ ![]() ,
, ![]() ];
];
(2)解:由题意知,要求铺路总费用最低,只要求△OEF的周长l的最小值即可.
由(1)得,l= ![]() ,α∈[
,α∈[ ![]() ,
, ![]() ],
],
设sinα+cosα=t,则sinαcosα= ![]() ,
,
∴l= ![]() =
= ![]()
由t=sinα+cosα= ![]() sin(α+
sin(α+ ![]() ),
),
又 ![]() ≤α+
≤α+ ![]() ≤
≤ ![]() ,得
,得 ![]() ,
,
∴ ![]() ,
,
从而当α= ![]() ,即BE=25时,lmin=50(
,即BE=25时,lmin=50( ![]() +1),
+1),
所以当BE=AF=25米时,铺路总费用最低,最低总费用为200000( ![]() +1)元
+1)元
【解析】(1)要将△OEF的周长l表示成α的函数关系式,需把△OEF的三边分别用含有α的关系式来表示,而OE,OF,分别可以在Rt△OBE,Rt△OAF中求解,利用勾股定理可求EF,从而可求.(2)要求铺路总费用最低,只要求△OEF的周长l的最小值即可.由(1)得l= ![]() ,α∈[
,α∈[ ![]() ,
, ![]() ],利用换元,设sinα+cosα=t,则sinαcosα=
],利用换元,设sinα+cosα=t,则sinαcosα= ![]() ,从而转化为求函数在闭区间上的最小值.
,从而转化为求函数在闭区间上的最小值.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin( ![]() ﹣φ)(0<φ<
﹣φ)(0<φ< ![]() )的图象经过点(0,﹣1).
)的图象经过点(0,﹣1).
(1)求函数f(x)的对称轴方程及相邻两条对称轴间的距离d;
(2)设α、β∈[0, ![]() ],f(3α+
],f(3α+ ![]() )=
)= ![]() ,f(3β+2π)=
,f(3β+2π)= ![]() ,求cos(α+β)的值.
,求cos(α+β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1).当![]() 时,求
时,求![]() 的单调增区间;
的单调增区间;
(2)当![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 的图象始终在直线
的图象始终在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn,且满足a1=2,anan+1=2(Sn+1) (![]() ).
).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,![]() (
(![]() ,
,![]() ),求{bn}的前n项和Tn;
),求{bn}的前n项和Tn;
(3)若数列{cn}满足![]() ,
,![]() (
(![]() ,
,![]() ),试问是否存在正整数p,q(其中1 < p < q),使c1,cp,cq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
),试问是否存在正整数p,q(其中1 < p < q),使c1,cp,cq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)ln x-a(x-1).
(1)当a=4时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)若当x∈(1,+∞)时,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.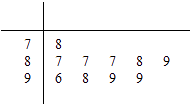
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com