
分析 根据题意,分2步进行分析:先安排奇数日的出行,由分步计数原理可得情况数目,再安排偶数日出行,分两种情况讨论即安排甲和不安排甲的车,将其相加可得此时的情况数目;由分步计数原理计算可得答案.
解答 解:根据题意,4月1日至5日,有3天奇数日,2天偶数日;
分2步进行分析:
①、安排奇数日出行,每天都有2种选择,共有23=8种,
②、安排偶数日出行,分两种情况讨论,
第一类,先选1天安排甲的车,另外一天安排其它车,有2×2=4种,
第二类,不安排甲的车,每天都有2种选择,共有22=4种,共计4+4=8,
根据分步计数原理,不同的用车方案种数共有8×8=64,
故答案为:64.
点评 本题考查排列、组合的应用,涉及分步和分类计数原理,关键是掌握如何分步讨论和分类分析.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
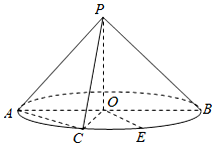 如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2$\sqrt{2}$.
如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com