
分析 根据三角形内角和定理求出∠ACB+∠ABC,求出∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB),求出∠OBC+∠OCB的度数,根据三角形的内角和定理求出∠BOC,由余弦定理,基本不等式可求OB•OC≤$\frac{1}{2(1-cos105°)}$,进而利用三角形面积公式即可计算得解.
解答 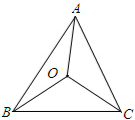 解:∵∠BAC=30°,
解:∵∠BAC=30°,
∴∠ABC+∠ACB=180°-30°=150°,
∵点O是△ABC的内心,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×150°=75°,
∴∠BOC=180°-75°=105°.
∵BC=1,
∴由余弦定理可得:1=OB2+OC2-2•OB•OC•cos105°≥2OB•OC-2•OB•OC•cos105°,整理可得:OB•OC≤$\frac{1}{2(1-cos105°)}$,
∴S△OBC=$\frac{1}{2}$OB•OC•sin105°≤$\frac{1}{2}×$$\frac{1}{2(1-cos105°)}$×sin105°=$\frac{sin105°}{4(1-cos105°)}$=$\frac{cos52.5°}{4sin52.5°}$=$\frac{1}{4}$cot52.5°.
故答案为:$\frac{1}{4}$cot52.5°.
点评 本题考查了三角形的内角和定理,余弦定理,基本不等式,三角形面积公式,三角形的内切圆与内心的应用,关键是求出∠OBC+∠OCB的度数,题目比较典型,难度适中.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{m+1}{m-1}$ | B. | $\frac{m-1}{m}$ | C. | $\frac{m-1}{m+1}$ | D. | $\frac{m}{m-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 纯虚数 | B. | 实数 | C. | 虚数 | D. | 以上都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{143}$ | B. | $\frac{1}{143}$ | C. | $\frac{24}{13}$ | D. | $\frac{6}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月收入(单位:百元) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 5 | 20 | 30 | 31 | 10 | 4 |
| 赞成人数 | 2 | 14 | 24 | 30 | 7 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com