
| A. | 纯虚数 | B. | 实数 | C. | 虚数 | D. | 以上都有可能 |
分析 设z1=a1+b1i(a1,b1∈R),z2=a2+b2i(a2,b2∈R),然后代入${z}_{1}•\overline{{z}_{2}}+\overline{{z}_{1}}•{z}_{2}$,由复数代数形式的乘除运算化简得答案.
解答 解:设z1=a1+b1i(a1,b1∈R),z2=a2+b2i(a2,b2∈R),
则${z}_{1}•\overline{{z}_{2}}+\overline{{z}_{1}}•{z}_{2}$=(a1+b1i)(a2-b2i)+(a1-b1i)(a2+b2i)=2a1a2+2b1b2.
∴${z}_{1}•\overline{{z}_{2}}+\overline{{z}_{1}}•{z}_{2}$是实数.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
| 日需求量 | 7 | 8 | 9 | 10 | 11 | 12 |
| 频数 | 5 | 7 | 10 | 14 | 10 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
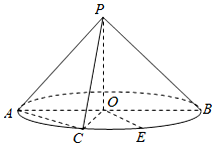 如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2$\sqrt{2}$.
如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
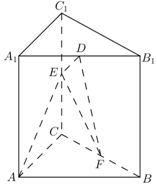 如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点.
如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com