
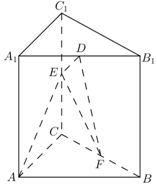
 如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点.
如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点. 分析 (1)以A为坐标原点、AB为x轴、AC为y轴、AA1为z轴建立如图的空间直角坐标系.求出相关的坐标,利用向量的数量积为0,证明$\overrightarrow{AE}⊥\overrightarrow{DF}$,推出AE⊥DF.
(2)求出平面DEF的一个法向量,设AE与平面DEF所成角为θ,利用向量的数量积求解AE与平面DEF所成角,然后求解点A到平面DEF的距离.
解答 解:(1)以A为坐标原点、AB为x轴、AC为y轴、AA1为z轴建立如图的空间直角坐标系.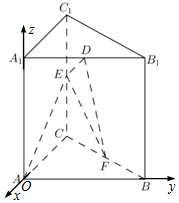
由题意可知A(0,0,0),D(0,1,2),E(-2,0,1),F(-1,1,0),
故$\overrightarrow{AE}=(-2,0,1),\overrightarrow{DF}=(-1,0,-2)$,…(4分)
由$\overrightarrow{AE}•\overrightarrow{DF}=-2×(-1)+1×(-2)=0$,
可知$\overrightarrow{AE}⊥\overrightarrow{DF}$,即AE⊥DF. …(6分)
(2)设$\overrightarrow n=(x,y,1)$是平面DEF的一个法向量,
又$\overrightarrow{DF}=(-1,0,-2),\overrightarrow{EF}=(1,1,-1)$,
故由$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{DF}=-x-2=0}\\{\overrightarrow n•\overrightarrow{EF}=x+y-1=0}\end{array}}\right.$解得$\left\{{\begin{array}{l}{x=-2}\\{y=3}\end{array}}\right.$故$\overrightarrow n=(-2,3,1)$. …(9分)
设AE与平面DEF所成角为θ,则$sinθ=\frac{{|\overrightarrow n•\overrightarrow{AE}|}}{{|\overrightarrow n|•|\overrightarrow{AE}|}}=\frac{5}{{\sqrt{14}•\sqrt{5}}}=\frac{{\sqrt{70}}}{14}$,…(12分)
所以AE与平面DEF所成角为$arcsin\frac{{\sqrt{70}}}{14}$,
点A到平面DEF的距离为$AE•sinθ=\frac{5}{14}\sqrt{14}$. …(14分)
点评 本题考查直线与平面所成角的求法,直线与直线垂直的判定方法,考查空间想象能力以及计算能力.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
| 水果产量(kg) | 3000 | 4000 |
| 概率 | 0.4 | 0.6 |
| 水果市场价格(元/kg) | 16 | 20 |
| 概率 | 0.5 | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 纯虚数 | B. | 实数 | C. | 虚数 | D. | 以上都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{143}$ | B. | $\frac{1}{143}$ | C. | $\frac{24}{13}$ | D. | $\frac{6}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | y=±$\frac{\sqrt{6}}{3}$x | C. | y=±$\frac{\sqrt{6}}{4}$x | D. | y=±$\frac{\sqrt{6}}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\overrightarrow{SF}=λ\overrightarrow{SC}$,SA∥平面BEF.
已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\overrightarrow{SF}=λ\overrightarrow{SC}$,SA∥平面BEF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com