
 已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\overrightarrow{SF}=λ\overrightarrow{SC}$,SA∥平面BEF.
已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\overrightarrow{SF}=λ\overrightarrow{SC}$,SA∥平面BEF.分析 (Ⅰ)连接AC,设AC∩BE=G,证明SA∥FG,通过△GEA~△GBC,求解λ即可.
(Ⅱ)以EA,EB,ES所在直线分别为x轴,y轴,z轴建立空间直角坐标系,求出平面SEB的法向量,平面EFB的法向量,利用空间向量的数量积求解所求二面角的余弦值.
解答 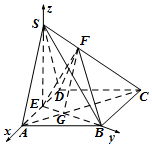 解:(Ⅰ)连接AC,设AC∩BE=G,
解:(Ⅰ)连接AC,设AC∩BE=G,
则平面SAC∩平面EFB=FG,
∵SA∥平面EFB,∴SA∥FG,∵△GEA~△GBC,
∴$\frac{AG}{GC}=\frac{AE}{BC}=\frac{1}{2}$,∴$\frac{SF}{FC}=\frac{AG}{GC}=\frac{1}{2}⇒SF=\frac{1}{3}SC$,
∴$λ=\frac{1}{3}$;
(Ⅱ)∵$SA=SD=\sqrt{5}$,∴SE⊥AD,SE=2,
又∵AB=AD=2,∠BAD=60°,∴$BE=\sqrt{3}$∴SE2+BE2=SB2,∴SE⊥BE,∴SE⊥平面ABCD,
以EA,EB,ES所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则$A(1,0,0),B(0,\sqrt{3},0),S(0,0,2)$,平面SEB的法向量$\overrightarrow m=\overrightarrow{EA}=(1,0,0)$,
设平面EFB的法向量$\overrightarrow n=(x,y,z)$,
则$\overrightarrow n⊥EB⇒(x,y,z)•(0,\sqrt{3},0)=0⇒y=0$,$\overrightarrow n⊥\overrightarrow{GF}⇒\overrightarrow n⊥\overrightarrow{AS}⇒(x,y,z)•(-1,0,2)=0⇒x=2z$,
令z=1,得$\overrightarrow n=(2,0,1)$,∴$cos<\overrightarrow m,\overrightarrow n>=\frac{\overrightarrow m•\overrightarrow n}{|\overrightarrow m|•|\overrightarrow n|}=\frac{{2\sqrt{5}}}{5}$,
即所求二面角的余弦值是$\frac{{2\sqrt{5}}}{5}$.
点评 本题考查空间向量的数量积的应用,二面角的平面角的求法,直线与平面的位置关系的应用,考查空间想象能力以及计算能力.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
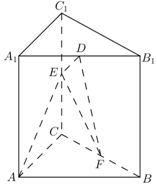 如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点.
如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
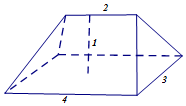 《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).
《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).| A. | 5立方丈 | B. | 6立方丈 | C. | 7立方丈 | D. | 9立方丈 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | [1,2] | C. | {0,1,2,4} | D. | [0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 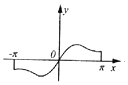 | C. | 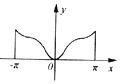 | D. | 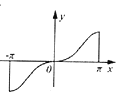 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com