
 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD.
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD.分析 (I)取CD的中点O,连接OB,OM,则可证OM∥AB,由CD⊥OM,CD⊥OB得出CD⊥平面ABOM,于是CD⊥AM;
(II)以O为原点建立空间直角坐标系,求出$\overrightarrow{AM}$和平面BDM的法向量$\overrightarrow{n}$,则直线AM与平面BDM所成角的正弦值为|cos<$\overrightarrow{AM},\overrightarrow{n}$>|.
解答 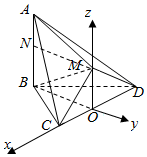 (Ⅰ)证明:取CD的中点O,连接OB,OM.
(Ⅰ)证明:取CD的中点O,连接OB,OM.
∵△BCD是等边三角形,
∴OB⊥CD.
∵△CMD是等腰直角三角形,∠CMD=90°,
∴OM⊥CD.
∵平面CMD⊥平面BCD,平面CMD∩平面BCD=CD,OM?平面CMD,
∴OM⊥平面BCD.
又∵AB⊥平面BCD,
∴OM∥AB.
∴O,M,A,B四点共面.
∵OB∩OM=O,OB?平面OMAB,OM?平面OMAB,
∴CD⊥平面OMAB.∵AM?平面OMAB,
∴CD⊥AM.
(Ⅱ)作MN⊥AB,垂足为N,则MN=OB.
∵△BCD是等边三角形,BC=2,
∴$OB=\sqrt{3}$,CD=2.
在Rt△ANM中,$AN=\sqrt{A{M^2}-M{N^2}}=\sqrt{A{M^2}-O{B^2}}=1$.
∵△CMD是等腰直角三角形,∠CMD=90°,
∴$OM=\frac{1}{2}CD=1$.
∴AB=AN+NB=AN+OM=2.
以点O为坐标原点,以OC,BO,OM为坐标轴轴建立空间直角坐标系O-xyz,
则M(0,0,1),$B({0,-\sqrt{3},0})$,D(-1,0,0),$A({0,-\sqrt{3},2})$.
∴$\overrightarrow{AM}=({0,\sqrt{3},-1})$,$\overrightarrow{BM}=({0,\sqrt{3},1})$,$\overrightarrow{BD}=({-1,\sqrt{3},0})$.
设平面BDM的法向量为$\overrightarrow{n}$=(x,y,z),
由n•$\overrightarrow{BM}=0$,n•$\overrightarrow{BD}=0$,∴$\left\{\begin{array}{l}{\sqrt{3}y+z=0}\\{-x+\sqrt{3}y=0}\end{array}\right.$,
令y=1,得$\overrightarrow{n}$=$({\sqrt{3},1,-\sqrt{3}})$.
设直线AM与平面BDM所成角为θ,
则$sinθ=|{cos?\overrightarrow{AM},n>}|$=$\frac{{|{\overrightarrow{AM}•n}|}}{{|{\overrightarrow{AM}}||n|}}$=$\frac{{2\sqrt{3}}}{{2×\sqrt{7}}}=\frac{{\sqrt{21}}}{7}$.
∴直线AM与平面BDM所成角的正弦值为$\frac{{\sqrt{21}}}{7}$.
点评 本题考查了线面垂直的判定,线面角的计算,空间向量的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -4 | C. | $-\frac{1}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
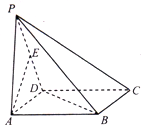 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1,a30 | B. | a1,a9 | C. | a10,a9 | D. | a10,a30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com