
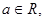 函数
函数 .
.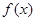 的单调区间和极值;
的单调区间和极值;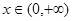 时,不等式
时,不等式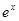
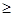
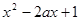 恒成立,求
恒成立,求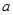 的范围.
的范围.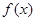 的单调递减区间
的单调递减区间 ,递增区间
,递增区间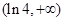 ,极小值为
,极小值为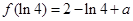 ,无极大值;(Ⅱ)
,无极大值;(Ⅱ)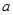 的范围是
的范围是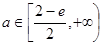 .
.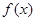 的单调区间和极值,研究单调性和极值问题,往往与导数有关,特别是极值,只能利用导数求得,故先对
的单调区间和极值,研究单调性和极值问题,往往与导数有关,特别是极值,只能利用导数求得,故先对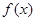 求导,得
求导,得 ,令
,令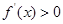 ,解得
,解得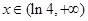 ,从而得递增区间,同样方法可得递减区间为
,从而得递增区间,同样方法可得递减区间为 ,进而得极值;(Ⅱ)当
,进而得极值;(Ⅱ)当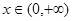 时,不等式
时,不等式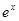
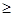
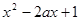 恒成立,求
恒成立,求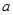 的范围,属于恒成立问题,解这一类题,常常采用含有参数
的范围,属于恒成立问题,解这一类题,常常采用含有参数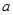 的放到不等式的一边,不含参数
的放到不等式的一边,不含参数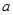 (即含
(即含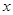 )的放到不等式的另一边,转化为函数的最值问题,故原不等式可化为
)的放到不等式的另一边,转化为函数的最值问题,故原不等式可化为
 ,只需求出
,只需求出 在
在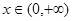 上的最大值即可,因含有
上的最大值即可,因含有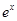 ,可通过求导来求,令
,可通过求导来求,令 可得
可得 ,
,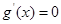 ,得
,得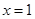 ,故
,故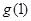 最大,最大值为
最大,最大值为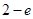 ,从而得
,从而得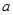 的范围.
的范围.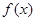 的单调递减区间
的单调递减区间 ,递增区间
,递增区间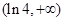 .极小值为
.极小值为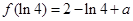 ,无极大值;
,无极大值;
 ,令
,令 可得
可得 ,令
,令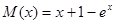 ,可得
,可得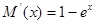 在
在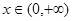 上恒小于等于零,所以函数g(x)=
上恒小于等于零,所以函数g(x)=  在(0,1)上递增,在(1,+
在(0,1)上递增,在(1,+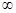 )递减,所以函数g(x)在
)递减,所以函数g(x)在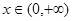 上有最大值g(1)=2-e,所求
上有最大值g(1)=2-e,所求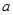 的范围是
的范围是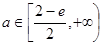


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com