
| A. | $-\frac{3}{2}$ | B. | $-\frac{5}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{3}$ |
分析 由已知向量的坐标求得向量$\overrightarrow{c}$的坐标,然后由向量垂直的坐标表示列式求得k的值.
解答 解:∵$\overrightarrow a=({1,2}),\overrightarrow b=({1,1}),\overrightarrow c=\overrightarrow a+k\overrightarrow b$,
∴$\overrightarrow{c}=(1,2)+k(1,1)=(1+k,2+k)$,
又$\overrightarrow b⊥\overrightarrow c$,∴1×(1+k)+1×(2+k)=0,
即2k+3=0,解得:k=-$\frac{3}{2}$.
故选:A.
点评 本题考查平面向量的数量积运算,考查了数量积的坐标表示,是基础题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | ($\frac{1}{2}$,+∞) | C. | ($\frac{1}{2}$,+1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,8] | B. | [$\frac{1}{2}$,3] | C. | [3,8] | D. | [$\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)和g(x)是两个定义在区间M上的函数,若对任意的x∈M,存在常数x0∈M,使的f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0),则称f(x)与g(x)在区间M上是“相似函数”,若f(x)=2x3-3(a+1)x2+6ax+b与g(x)=x+$\frac{4}{x}$在区间[1,3]上是“相似函数”,则a,b的值分别是( )
已知函数f(x)和g(x)是两个定义在区间M上的函数,若对任意的x∈M,存在常数x0∈M,使的f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0),则称f(x)与g(x)在区间M上是“相似函数”,若f(x)=2x3-3(a+1)x2+6ax+b与g(x)=x+$\frac{4}{x}$在区间[1,3]上是“相似函数”,则a,b的值分别是( )| A. | a=-2,b=0 | B. | a=-2,b=-2 | C. | a=2,b=0 | D. | a=2,b=-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
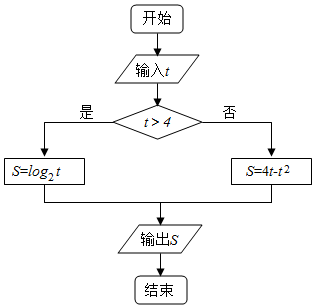
| A. | (-∞,1) | B. | [1,4] | C. | (-∞,1]∪(4,+∞) | D. | (-∞,1]∪[4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{11}{8}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com