
【题目】已知函数![]() (
(![]() 为实常数且
为实常数且![]() ).
).
(Ⅰ)当![]() 时;
时;
①设![]() ,判断函数
,判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
②求证:函数![]() 在
在![]() 上是增函数;
上是增函数;
(Ⅱ)设集合![]() ,若
,若![]() ,求
,求![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
【答案】(Ⅰ)①见解析,②见解析,(Ⅱ)![]()
【解析】
(Ⅰ)①确定函数的解析式,然后利用函数的定义域,及g(-x)=g(x),g判断函数的奇偶性;②利用二次函数与复合函数的单调性的,可证得函数的单调性
(Ⅱ)将原问题转化为恒成立的问题,结合恒成立的条件即可求得实数λ的范围.
(Ⅰ)①函数为偶函数,证明如下:
当a=1,b=3时,![]() ,∴g(x)=f(x+2)=
,∴g(x)=f(x+2)=![]() ,
,
其定义域为{x|x≠1且x≠-1},函数的定义域关于坐标原点对称,
g(-x)=![]() =g(x),故g(x)是偶函数.
=g(x),故g(x)是偶函数.
②![]() ,
,
令u(x)=![]() ,
,
易知u(x)在![]() 上是增函数,u(x)的值域为[-1,0), f(u)=
上是增函数,u(x)的值域为[-1,0), f(u)=![]() 在[-1,0)上增函数,故
在[-1,0)上增函数,故![]() 在
在![]() 上是增函数.
上是增函数.
(Ⅱ)因为M∩N=,所以函数y=f(x)与y=![]() 的图象无公共点,
的图象无公共点,
即方程![]() (﹡)无无实解,
(﹡)无无实解,
![]() ,
,
当λ=0时,方程无解,显然符合题意,
当λ≠0时,令y=(xa)(xb)![]() =
=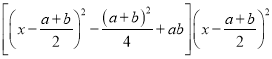 ,
,
令t=![]() ,则y=
,则y=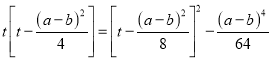 ,
,
当t=![]() 时,ymin=
时,ymin=![]() ,
,
所以,要使(﹡)无实数解,只要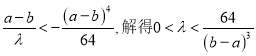 ,
,
综上,![]()


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】2019年第十三届女排世界杯共12支参赛球队,比赛赛制釆取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以3—0或3—1取胜的球队积3分,负队积0分;而在比赛中以3—2取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为![]() .
.
(1)第10轮比赛中,记中国队3—1取胜的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() .
.
(2)以(1)中的![]() 作为
作为![]() 的值.
的值.
(i)在第10轮比赛中,中国队所得积分为![]() ,求
,求![]() 的分布列;
的分布列;
(ⅱ)已知第10轮美国队积3分,判断中国队能否提前一轮夺得冠军(第10轮过后,无论最后一轮即第11轮结果如何,中国队积分最多)?若能,求出相应的概率;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F(0,1)为平面上一点,H为直线l:y=﹣1上任意一点,过点H作直线l的垂线m,设线段FH的中垂线与直线m交于点P,记点P的轨迹为Γ.
(1)求轨迹Γ的方程;
(2)过点F作互相垂直的直线AB与CD,其中直线AB与轨迹Γ交于点AB,直线CD与轨迹Γ交于点CD,设点M,N分别是AB和CD的中点.
①问直线MN是否恒过定点,如果经过定点,求出该定点,否则说明理由;
②求△FMN的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,底面
中,底面![]() 是等腰梯形,
是等腰梯形,![]() ,顶点
,顶点![]() 在底面
在底面![]() 内的射影恰为点
内的射影恰为点![]() .
.
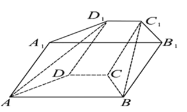
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来电子商务蓬勃发展,同时也极大地促进了快递行业的发展,为了更好地服务客户,某快递公司使用客户评价系统对快递服务人员的服务进行评价,每月根据客户评价评选出“快递之星”.已知“快递小哥”小张在每个月被评选为“快递之星”的概率都是![]() ,则小张在第一季度的3个月中有2个月都被评为“快递之星”的概率为_______;设小张在上半年的6个月中被评为“快递之星”的次数为随机变量X,则随机变量X的方差
,则小张在第一季度的3个月中有2个月都被评为“快递之星”的概率为_______;设小张在上半年的6个月中被评为“快递之星”的次数为随机变量X,则随机变量X的方差![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
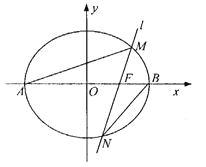
【题目】如图,已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点,过右焦点
的左、右顶点,过右焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com