
【题目】在极坐标系中,已知点![]() 到直线
到直线![]() 的距离为3.
的距离为3.
(1)求实数![]() 的值;
的值;
(2)设![]() 是直线
是直线![]() 上的动点,
上的动点,![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 轨迹方程,并指出轨迹是什么图形.
轨迹方程,并指出轨迹是什么图形.
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且y=f(x)图象的两相邻对称轴间的距离为
sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且y=f(x)图象的两相邻对称轴间的距离为![]() ,则f(
,则f(![]() )的值为( )
)的值为( )
A.﹣1B.1C.![]() .D.
.D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|﹣|x﹣5|.
(1)当a=2时,求证:﹣3≤f(x)≤3;
(2)若关于x的不等式f(x)≤x2﹣8x+20在R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数且
为实常数且![]() ).
).
(Ⅰ)当![]() 时;
时;
①设![]() ,判断函数
,判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
②求证:函数![]() 在
在![]() 上是增函数;
上是增函数;
(Ⅱ)设集合![]() ,若
,若![]() ,求
,求![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,已知可引起感冒以及中东呼吸综合征![]() 和严重急性呼吸综合征
和严重急性呼吸综合征![]() 等较严重疾病.而今年初出现并在全球蔓延的新型冠状病毒
等较严重疾病.而今年初出现并在全球蔓延的新型冠状病毒![]() 是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
某药物研究所为筛查该种病毒,需要检验血液是否为阳性,现有![]() (
(![]() ,且
,且![]() )份血液样本,每个样本取到的可能性相等,有以下两种检验方式:
)份血液样本,每个样本取到的可能性相等,有以下两种检验方式:
方式一:逐份检验则需要检验![]() 次;
次;
方式二:混合检验,将![]() 份血液样本分别取样混合在一起检验,若检验结果为阴性,则这
份血液样本分别取样混合在一起检验,若检验结果为阴性,则这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有6份血液样本,其中只有2份样本为阳性,从中任取3份样本进行医学研究,求至少有1份为阳性样本的概率;
(2)假设将![]() (
(![]() 且
且![]() )份血液样本进行检验,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本进行检验,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() ;
;
①运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() 与干扰素计量
与干扰素计量![]() 相关,其中数列
相关,其中数列![]() 满足
满足![]() ,当
,当![]() 时,试讨论采用何种检验方式更好?
时,试讨论采用何种检验方式更好?
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() ,设数列
,设数列![]() 、
、![]() 的前
的前![]() 项和分别为
项和分别为![]() 和
和![]() .
.
(1)若数列![]() 是等差数列,求
是等差数列,求![]() 和
和![]() ;
;
(2)若数列![]() 是公比为2的等比数列.
是公比为2的等比数列.
①求![]() ;
;
②是否存在实数![]() ,使
,使![]() 对任意自然数
对任意自然数![]() 都成立?若存在,求
都成立?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知等边![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .如图2,将
.如图2,将![]() 沿
沿![]() 折起到
折起到![]() 的位置.
的位置.
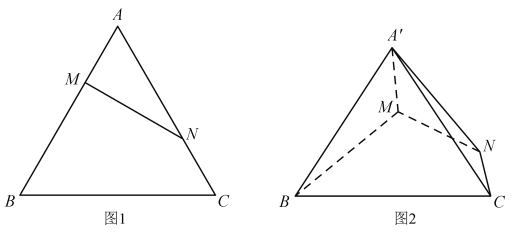
(1)求证:平面![]() 平面
平面![]() ;
;
(2)给出三个条件:①![]() ;②二面角
;②二面角![]() 大小为
大小为![]() ;③
;③![]() 到平面
到平面![]() 的距离为
的距离为![]() .在中任选一个,补充在下面问题的条件中,并作答:
.在中任选一个,补充在下面问题的条件中,并作答:
在线段![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 的体积为
的体积为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
注:如果多个条件分别解答,按第一个解答给分。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com