
【题目】冠状病毒是一个大型病毒家族,已知可引起感冒以及中东呼吸综合征![]() 和严重急性呼吸综合征
和严重急性呼吸综合征![]() 等较严重疾病.而今年初出现并在全球蔓延的新型冠状病毒
等较严重疾病.而今年初出现并在全球蔓延的新型冠状病毒![]() 是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
某药物研究所为筛查该种病毒,需要检验血液是否为阳性,现有![]() (
(![]() ,且
,且![]() )份血液样本,每个样本取到的可能性相等,有以下两种检验方式:
)份血液样本,每个样本取到的可能性相等,有以下两种检验方式:
方式一:逐份检验则需要检验![]() 次;
次;
方式二:混合检验,将![]() 份血液样本分别取样混合在一起检验,若检验结果为阴性,则这
份血液样本分别取样混合在一起检验,若检验结果为阴性,则这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有6份血液样本,其中只有2份样本为阳性,从中任取3份样本进行医学研究,求至少有1份为阳性样本的概率;
(2)假设将![]() (
(![]() 且
且![]() )份血液样本进行检验,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本进行检验,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() ;
;
①运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() 与干扰素计量
与干扰素计量![]() 相关,其中数列
相关,其中数列![]() 满足
满足![]() ,当
,当![]() 时,试讨论采用何种检验方式更好?
时,试讨论采用何种检验方式更好?
参考数据:![]() .
.
科目:高中数学 来源: 题型:
【题目】定义:![]() 是无穷数列,若存在正整数k使得对任意
是无穷数列,若存在正整数k使得对任意![]() ,均有
,均有![]() 则称
则称![]() 是近似递增(减)数列,其中k叫近似递增(减)数列
是近似递增(减)数列,其中k叫近似递增(减)数列![]() 的间隔数
的间隔数
(1)若![]() ,
,![]() 是不是近似递增数列,并说明理由
是不是近似递增数列,并说明理由
(2)已知数列![]() 的通项公式为
的通项公式为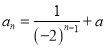 ,其前n项的和为
,其前n项的和为![]() ,若2是近似递增数列
,若2是近似递增数列![]() 的间隔数,求a的取值范围:
的间隔数,求a的取值范围:
(3)已知![]() ,证明
,证明![]() 是近似递减数列,并且4是它的最小间隔数.
是近似递减数列,并且4是它的最小间隔数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场进行抽奖促销活动,抽奖箱中有大小完全相同的4个小球,分别标有“A”“B”“C”“D”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“D”字球,则停止取球.获奖规则如下:依次取到标有““A”“B”“C”“D”字的球为一等奖;不分顺序取到标有“A”“B”“C”“D”字的球,为二等奖;取到的4个球中有标有“A”“B”“C”三个字的球为三等奖.
(1)求分别获得一、二、三等奖的概率;
(2)设摸球次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来电子商务蓬勃发展,同时也极大地促进了快递行业的发展,为了更好地服务客户,某快递公司使用客户评价系统对快递服务人员的服务进行评价,每月根据客户评价评选出“快递之星”.已知“快递小哥”小张在每个月被评选为“快递之星”的概率都是![]() ,则小张在第一季度的3个月中有2个月都被评为“快递之星”的概率为_______;设小张在上半年的6个月中被评为“快递之星”的次数为随机变量X,则随机变量X的方差
,则小张在第一季度的3个月中有2个月都被评为“快递之星”的概率为_______;设小张在上半年的6个月中被评为“快递之星”的次数为随机变量X,则随机变量X的方差![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
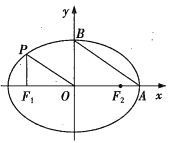
【题目】如图,过椭圆C:![]() 上一点P作x轴的垂线,垂足为
上一点P作x轴的垂线,垂足为![]() ,已知
,已知![]() ,
,![]() 分别为椭圆C的左、右焦点,A,B分别是椭圆C的右顶点、上顶点,且
分别为椭圆C的左、右焦点,A,B分别是椭圆C的右顶点、上顶点,且![]() ,
,![]() .
.
(1)求椭圆C的方程;
(2)过点![]() 的直线l交椭圆C于M,N两点,记直线PM,PN,MN的斜率分别为
的直线l交椭圆C于M,N两点,记直线PM,PN,MN的斜率分别为![]() ,问:
,问:![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() .已知函数
.已知函数![]() ,
,![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)已知函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,
(i)求证:![]() 在
在![]() 处的导数等于0;
处的导数等于0;
(ii)若关于x的不等式![]() 在区间
在区间![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点下的距离为10.
到其焦点下的距离为10.
(1)求抛物线C的方程;
(2)设过焦点F的的直线![]() 与抛物线C交于
与抛物线C交于![]() 两点,且抛物线在
两点,且抛物线在![]() 两点处的切线分别交x轴于
两点处的切线分别交x轴于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com