
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,判断函数
时,判断函数![]() 的零点个数;
的零点个数;
(Ⅱ)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)函数![]() 的零点个数为1;(Ⅱ)
的零点个数为1;(Ⅱ)![]()
【解析】
(Ⅰ)根据题意,代入![]() ,对函数求导,判断函数单调性,根据特殊值
,对函数求导,判断函数单调性,根据特殊值![]() ,即可判断零点个数;
,即可判断零点个数;
(Ⅱ)根据题意,解决函数![]() 恒成立问题,方法一:转化
恒成立问题,方法一:转化![]() 对任意
对任意![]() 恒成立,则有
恒成立,则有![]() 对任意
对任意![]() 恒成立,构造函数
恒成立,构造函数![]() ,只需求
,只需求![]() ,利用导数研究函数最值问题。方法二:
,利用导数研究函数最值问题。方法二:![]() 对任意
对任意![]() 恒成立.构造函数
恒成立.构造函数![]() ,转化成射线
,转化成射线![]() 与函数
与函数![]() 的图象相切时属临界状态,计算求解;方法三:含参的函数最小值探究,只需
的图象相切时属临界状态,计算求解;方法三:含参的函数最小值探究,只需![]() ,即可求解参数取值范围.
,即可求解参数取值范围.
(Ⅰ)当![]() 时,
时,![]() ,其定义域为
,其定义域为![]() ,
,
求导得![]() ,
,
于是当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,又
单调递增,又![]() ,所以函数
,所以函数![]() 的零点个数为1;
的零点个数为1;
(Ⅱ)法1:因对任意![]() ,
,![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,于是
恒成立,于是![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,只需
,只需![]() .
.
对函数![]() 求导,得
求导,得![]() ,令
,令![]() ,
,
则![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以当
,所以当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 单调递增,所以函数
单调递增,所以函数![]() ,于是
,于是![]() ,即实数
,即实数![]() 的取值范围为
的取值范围为![]() .
.
法2:因对任意![]() ,
,![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立.构造函数
恒成立.构造函数![]() ,对其求导,得
,对其求导,得![]() ,
,
令![]() ,得
,得![]() (
(![]() 舍去),所以当
舍去),所以当 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当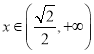 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
函数![]() 的图象是一条过原点的射线(不包括端点),旋转射线(不含端点),发现
的图象是一条过原点的射线(不包括端点),旋转射线(不含端点),发现![]() 与函数
与函数![]() 的图象相切时属临界状态.
的图象相切时属临界状态.
设切点为![]() ,则
,则![]() ,整理得
,整理得![]() ,
,
显然![]() 在
在![]() 上是增函数,又
上是增函数,又![]() ,所以
,所以![]() ,此时切线斜率为1,结合图象,可知实数
,此时切线斜率为1,结合图象,可知实数![]() 的取值范围为
的取值范围为![]() .
.
法3:根据题意只需![]() 即可.
即可.
又![]() ,令
,令![]() ,因2与
,因2与![]() 异号,所以必有一正根,不妨设为
异号,所以必有一正根,不妨设为![]() ,则
,则![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,所以
单调递增,所以![]() ,
,
又![]() 在
在![]() 上是减函数,又
上是减函数,又![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() 在
在![]() 上单调递增,则实数
上单调递增,则实数![]() 的取值范围为
的取值范围为![]() .
.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数且
为实常数且![]() ).
).
(Ⅰ)当![]() 时;
时;
①设![]() ,判断函数
,判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
②求证:函数![]() 在
在![]() 上是增函数;
上是增函数;
(Ⅱ)设集合![]() ,若
,若![]() ,求
,求![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形ABCD是矩形,平面
中,四边形ABCD是矩形,平面![]() 平面ABCD,
平面ABCD,![]() ,E是SB的中点,M是CD上任意一点.
,E是SB的中点,M是CD上任意一点.
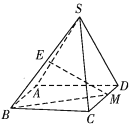
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 平面SAD,求直线BM与平面SAB所成角的正弦值.
平面SAD,求直线BM与平面SAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() ,设数列
,设数列![]() 、
、![]() 的前
的前![]() 项和分别为
项和分别为![]() 和
和![]() .
.
(1)若数列![]() 是等差数列,求
是等差数列,求![]() 和
和![]() ;
;
(2)若数列![]() 是公比为2的等比数列.
是公比为2的等比数列.
①求![]() ;
;
②是否存在实数![]() ,使
,使![]() 对任意自然数
对任意自然数![]() 都成立?若存在,求
都成立?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇响应“绿水青山就是金山银山”的号召,因地制宜的将该镇打造成“生态水果特色小镇”.经调研发现:某珍稀水果树的单株产量![]() (单位:千克)与施用肥料
(单位:千克)与施用肥料![]() (单位:千克)满足如下关系:
(单位:千克)满足如下关系: ,肥料成本投入为
,肥料成本投入为![]() 元,其它成本投入(如培育管理、施肥等人工费)
元,其它成本投入(如培育管理、施肥等人工费)![]() 元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为
元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为![]() (单位:元).
(单位:元).
(Ⅰ)求![]() 的函数关系式;
的函数关系式;
(Ⅱ)当施用肥料为多少千克时,该水果树的单株利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,点
,点![]() 是椭圆
是椭圆![]() 上除长轴端点外的任一点,连接
上除长轴端点外的任一点,连接![]() ,
,![]() ,设
,设![]() 的内角平分线
的内角平分线![]() 交
交![]() 的长轴于点
的长轴于点![]() .
.
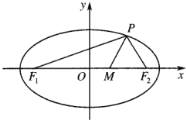
(Ⅰ)求实数![]() 的取值范围;
的取值范围;
(Ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲,乙两种不透明充气包装的袋装零食,每袋零食甲随机附赠玩具![]() ,
,![]() ,
,![]() 中的一个,每袋零食乙从玩具
中的一个,每袋零食乙从玩具![]() ,
,![]() 中随机附赠一个.记事件
中随机附赠一个.记事件![]() :一次性购买
:一次性购买![]() 袋零食甲后集齐玩具
袋零食甲后集齐玩具![]() ,
,![]() ,
,![]() ;事件
;事件![]() :一次性购买
:一次性购买![]() 袋零食乙后集齐玩具
袋零食乙后集齐玩具![]() ,
,![]() .
.
(1)求概率![]() ,
,![]() 及
及![]() ;
;
(2)已知![]() ,其中
,其中![]() ,
,![]() 为常数,求
为常数,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为正项数列
为正项数列![]() 的前
的前![]() 项和,满足
项和,满足![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若不等式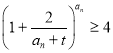 对任意正整数
对任意正整数![]() 都成立,求实数
都成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() (其中
(其中![]() 是自然对数的底数),求证:
是自然对数的底数),求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com